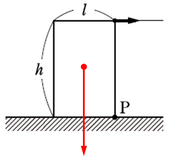
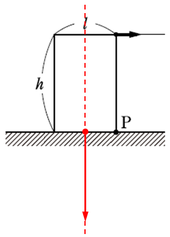
点\(P\)を回転の中心とすると、重力による力のモーメントは反時計回り(左回り)、外力による力のモーメントは時計回り(右回り)に加わっていることが分かります。
いま、この問題では、外力を加えすぎると物体が回転します、その瞬間は外力がどのくらいの大きさのときですか、と問うていますね。
重力による力のモーメントより外力による力のモーメントが大きくなった時に、物体が回転しますので、物体が傾き始める瞬間は両者が等しくなったときです。
よって、
(左回りのモーメント)\(=\)(右回りのモーメント) より
\(mg×\displaystyle\frac{l}{2}\)\(=\)\(T×h\)
\(T=\displaystyle\frac{mgl}{2h}\)
となります。
(2)
ですが、(1)の条件が満たされるためには、前提として、外力を加えても物体が滑らないくらい強い摩擦面に置かれていなければなりません。ここでは、物体が回転するまでに滑らないためにはどのくらい強い摩擦面でなければならないかが問われています。
両方の条件を満たしたときにだけ、この実験が成功します。
解くこと自体は物理基礎の最大摩擦の問題のレベルですので、そんなに難しくはありません。
最大摩擦力(最大静止摩擦力)は\(f_0=\mu N\)で表されます。ここでは垂直抗力の大きさは\(N=mg\)ですので、いきなり\(f_0=\mu mg\)としてしまう方が早いですね。
最大摩擦力というのは、「それより大きい力を加えると物体が動く」という意味を持ちますので、物体が動かないためには、
(加えた力の大きさ)≦(最大摩擦力)
の関係が成立していればいいわけです。等号成立のときも、最大”静止”摩擦力が働いているので、まだ動きません。
よって、
\(T≦f_0\) より
\(\displaystyle\frac{mgl}{2h}≦\mu mg\)
\(\displaystyle\frac{l}{2h}≦\mu\)
という関係が成立していればいいことが分かります。
よく勘違いするのは、最大摩擦力の公式の\(f_0\)と外力の\(F\)を同じものだと錯覚してしまって、なんで\(f_0≦\mu N\)になるんだ?といった迷路に入ってしまうことです。最大摩擦力はあくまで最大摩擦力であって、問題で設定された外力の\(F\)と混同してしまわないように気をつけてください。