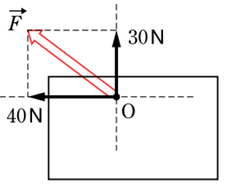
(a)
力の矢印は、力の大きさと向きを変えなければ、作用線上のどこに動かしても全く同じ物理現象となります。
なので、(a)の場合は、\(30N\)の力を少し上にずらし、\(40N\)の力は少し右にずらして、同じ作用点から力が働いている図に書き換えてやります。
すると、単純に\(30N\)の力と\(40N\)の力を三平方の定理を使って合成してやればいいので、合力は\(50N\)となります。
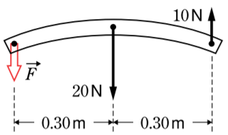
(b)
2力が平行で逆向きを向いているので、外分によって求めるのが早いです。
2力が\(20N\)と\(10N\)なので、\(2:1\)の質量比になっています。この逆比\(1:2\)となるような外分点に合力が作図されます。
まずそもそも外分点についてですが、「外」分というくらいですので、2力間の「内」側にはありません。\(20N\)の力の作用点より左か、\(10N\)の力の作用点より右に外分点が存在するはずです。
\(1:2\)に外分、となると、この図の場合であれば、\(20N\)の力から距離①、\(10N\)の力から距離②だけ離れた点が外分点ですので、外分点から見れば、\(10N\)の力の方が遠くにあることになります。つまり、外分点は図の左側に来るんだ、というところまでは即座に見破れるようにトレーニングしておきましょう。
位置は図の場所となります。
力の大きさは、瞬殺できます。図の上向きに\(10N\)、下向きに\(20N\)ですので、合力の大きさは下向きに\(10N\)です。力がどこからかかっているかは関係ありません。そのまま加減算で求めます。
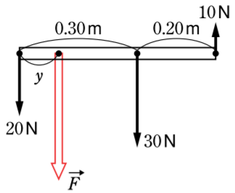
(c)
並行な力が何本か働いているときは、内分・外分を使って解くには手数が必要となり、めんどくさくなってきます。こういうときは、直接、力のモーメントのつり合いで求めてしまう方がいいでしょう。
合力の大きさは\(20[N]+30[N]-10[N]=40[N]\)です。
重心(合力の作用点)周りの力のモーメントのつり合いの式より、
\(20y = 30[N]×(0.30-y)[m] - 10[N]×(0.50-y)[m] \)
\(20y = 9-30y -5+10y\)
\(40y=4\)
\(y=0.10m\)
