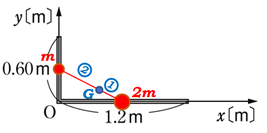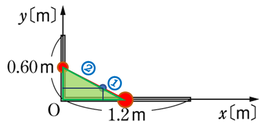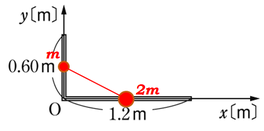
針金は一様なものを使っています。一様、というのは、どの部分も同じ材質、同じ質量、同じ太さ、といった状態のことを指していますので、\(1.8m\)の一様な針金を図のように、\(0.60m\)と\(1.2m\)になるように、長さが\(1:2\)となるように折り曲げると、質量も\(1:2\)となります。
仮に、\(y\)軸部分の針金の重さを\(m\)とおいてやると、\(x\)軸部分の針金の重さは\(2m\)となりますので、それぞれ、針金の中点に質量が集まっているとしておきましょう。
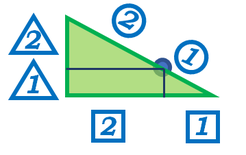
三角形部分だけアップしてみましょう。
辺の比はそれぞれ図のようになります。
ちょっと説明を省略しますが、ここから、座標は\((x,y)=(0.40m,0.10m)\)となりますね。