一様でない棒の重心はどこでしょう問題です。
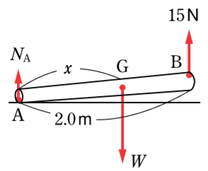
ふつうは、モーメントを使って解く問題です。重心の位置が不明なので、左端から\(x\)のところに重心あがあるとして、この点を\(G\)とします。すると、\(GB=2-x\)という長さもついでに出ますね。
初め、左端をついた状態で棒を引き上げます。図はすでにだいぶ持ち上げてしまっている図ですが、持ち上がり始めた瞬間は、棒とそれぞれの力はすべて垂直になっているので、それを利用して力のモーメントの式を立てます。棒の重さはわざわざ\(mg\)と2文字に分けず、単に\(W\)としておきます。問題文もそうなっていますね。左端周りの力のモーメントのつり合いの式は、
\(xW=2×15\)
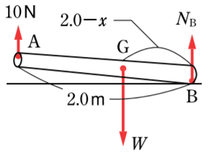
今度は右端をついた状態で棒を引き上げると、右端周りの力のモーメントのつり合いの式は、
\((2-x)W=2×10\)
これらを連立すると、
\(xW=30\)
\(2W-xW=20\)
ですので、1本目の式を2本目に代入して、
\(2W-30=20\)
\(2W=50\)
\(W=25[N]\)
この値を元の連立式のどちらかに代入して\(x\)も求めると、
\(x=1.2[m]\)
となります。
が、私はそんなやり方では解きません。
結局のところ同時に両端を持ち上げると、左端を持ち上げるときには\(10N\)、右端を持ち上げるときには\(15N\)必要だという設定なので、足して\(25N\)。
これが棒の重さ。よって\(W=25[N]\)。
また、その力の大きさが②:③なので、重心位置はその逆比の③:②に内分する点にあるはずなので、\(x=1.2[m]\)。
私なら、こちらのやり方で解きます。
