(1)
まず作図しましょう。
図から、水平方向の力のつり合いの式は
\(N_A=F\)
同じく、鉛直方向の力のつり合いの式は
\(N_B=W\)
となりますね。
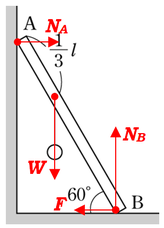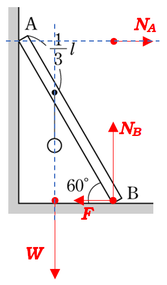
力の矢印は、作用線上であれば動かしても結果に影響がありませんので、計算する上で都合良い場所に移動します。
点\(B\)周りの力のモーメントのつり合いの式を立てるために、点\(B\)から力まで線を引いたときに、垂直になってくれるような場所まで力を移動させることにします。
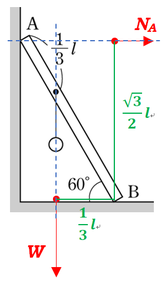
点\(B\)からの補助線と、長さを計算して書き入れると、図のようになります。
ここから、点\(B\)周りの力のモーメントのつり合いの式を立てると、
\(N_A×\)\(\displaystyle\frac{\sqrt{3}}{2}l\)\(=W×\)\(\displaystyle\frac{1}{3}l\)
となります。
(2)
あとは、３本の式を解くだけです。
\(N_B=W[N]\)
は、このまま答えとしていいですね。単位を付け忘れることがないように。
\(N_A×\)\(\displaystyle\frac{\sqrt{3}}{2}l\)\(=W×\)\(\displaystyle\frac{1}{3}l\)
より、両辺\(6\)倍して、ついでに\(l\)も払ってしまいましょう。
\(N_A×3\sqrt{3}=2W\)
\(N_A=\displaystyle\frac{2W}{3\sqrt{3}}\)
\(N_A=\displaystyle\frac{2\sqrt{3}W}{9}[N]\)
そうすると、
\(F=N_A=\displaystyle\frac{2\sqrt{3}W}{9}[N]\)
となり、これで全部出そろいますね。
