並行移動条件と回転移動条件に関する問題です。
剛体に外力を加えたとき
(Ⅰ)平行移動しないための条件
(加えた力) ≦ (最大静止摩擦力)
\(F≦\mu N\)
(Ⅱ)平行移動するための条件
(加えた力) > (最大静止摩擦力)
\(F>\mu N\)
(Ⅲ)回転しないための条件
(左回りの力のモーメント) = (右回りの力のモーメント)
(Ⅳ)回転するための条件
(左回りの力のモーメント) ≠ (右回りの力のモーメント)
が成立します。
この手の問題では、剛体に外力を加えたとき、剛体を動かしたい(ⅡかつⅢ)のか、剛体を回したい(ⅠかつⅣ)のかを問題文から読み取ってから、どういう式変形に進めばいいのかを考える必要があります。
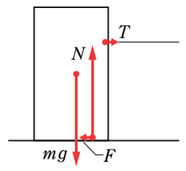
この問題では、どうやら物体を回転させずに平行移動させたいようです。
すると、必要な条件は「Ⅱ 平行移動する」かつ「Ⅲ 回転しない」を両方とも満たせばよいと分かります。
(ア)
まず、物体が平行移動するためには、物体に加えた力が、最大静止摩擦力よりも大きければ良いことになります。摩擦に関する数式処理では、剛体でも質点でも解き方は同じですので、図のように力を作図しておいて、外力と最大摩擦力の大小関係を比較しましょう。
最大摩擦力の公式は\(f_0=\mu N\)でした。今、鉛直方向の力のつり合いから、\(N=mg\)ですので、最大摩擦力の大きさは、
\(f_0=\mu mg\)
となります。これが何\(N\)を表すかは不明ですが、この値よりも大きい力で物体を引いてやると、物体を動かすことができます。
よって
\(T>\mu mg\)
となり、(ア)は\(\mu\)となりました。
これがまず「Ⅱ 平行移動する」ための条件となります。
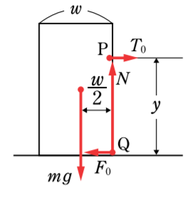
(イ)
次に、物体が引っ張られている間、物体が「Ⅲ 回転しない」ための条件を考えてみましょう。
外力\(T\)を大きくしていくと物体が回転し始めますが、回転するとなると、その回転中心は点\(Q\)になりますね。
なので、この点\(Q\)を中心とした力のモーメントを考えることにしましょう。
まず摩擦力\(F_0\)と垂直抗力\(N\)についてですが、これらは、物体が回転し始めるときに点\(Q\)にあります。なので力のモーメントの式を立てるとき、距離に相当する値が\(0\)となり、力のモーメントを考えなくてよくなります。
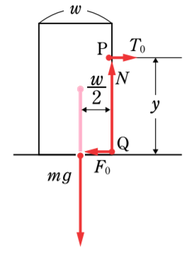
次に外力と重力についての力のモーメントを考えてみましょう。
点\(Q\)を中心として、外力は時計回り、重力は反時計回りに回転させようとする能力を持ちます。
物体が回転し始める瞬間では、まだ回転はしていません。
力のモーメントは同じ値になりますので、それぞれ求めて、等式にしてしまいましょう。
外力の力のモーメントは作図のまま使えそうですが、重力だけ使い勝手がいいように力をずらしておきます。力は向きと大きささえ変えなければ、作用線上であれば好きに動かしてもいいですので、元の図から少し下にずらして、作用点が床と接するところまで動かしてしまいます。
よって
(右回りの力のモーメント)=(左回りの力のモーメント)
(外力のモーメント)=(重力のモーメント)
\(T_0 × y = mg × \displaystyle\frac{w}{2}\)
\(T_0=\displaystyle\frac{mgw}{2y}\)
となりました。これが「Ⅲ 回転しない」ための条件となります。
2つの条件を同時に満たすためには、(ア)を求めるときの式の形から、同時に
\(T_0>\mu mg\)
でなければいけませんので、\(T_0\)を代入して、
\(\displaystyle\frac{mgw}{2y}>\mu mg\)
\(\displaystyle\frac{w}{2y}>\mu\)
\(w>2\mu y\)
\(\displaystyle\frac{w}{2\mu}>y\)
となればいいことが分かりました。不等式の変形過程は、もっとさっくり追える人は自分のやり方で追ってください。
