運動量と力積
歴史的な背景では、運動の程度を表す物理量がどのように表されるのか、長い議論がありました。
それを話し始めてしまうと、単なる歴史の授業になってしまいそうなので置いといて、ここでは結論から入ることにしましょう。
長い議論の末、物体同士の衝突のときに用いる「運動の程度」として、運動量という量が決定されました。
この運動量は、物体の質量\(m\)と、物体の速度\(v\)の積で表すことに決めました。
運動量の単位は、覚えません。\(m\)と\(v\)の積なので、\(m\)の単位\(kg\)と、\(v\)の単位\(m/s\)を単にひっつけて、間にドットを差し込むことで\([kg・m/s]\)と表します。暗記する、というよりも、単位を並べてしまう、という意識をもっておくと、むしろ覚えやすく、特に難しい話ではないかと思います。
運動量
\(p=mv\)
\(p\):運動量\([kg・m/s]\)
\(m\):物体の質量\([kg]\)
\(v\):物体の速度\([m/s]\)
物体に力がはたらくと、運動の法則から、物体は加速度をもつことになって、運動の様子を変えます。
このとき、加えた力が一定の大きさであれば、力を加えた時間が長いほど、それに比例して運動のようすは大きい変化となります。そこで、運動方程式ではなく、もっとシンプルに、力と時間の積という物理量を決めてしまいましょう。
物体が衝突するときの運動の様子の変化を考えるときには、この「力×時間」という物理量を使うと、とても便利になります。これを力積と呼びます。
力積の単位も、覚えません。運動量と同じようにして、力の単位\([N]\)と、時間の単位\([s]\)をドットで結んでやって、\([N・s]\)としてやるだけで完成です。
力積
\(I=F\Delta t\)
\(I\):力積\([N・s]\)
\(F\):加えた力\([N]\)
\(\Delta t\):力を加えた時間\([s]\)
運動量と力積の関係
運動方程式を学習したとき、いくつかの問題の解き方と、その流れはすでにマスターしつつあると思います。
ところで、運動方程式って何を求めるための方程式だったか覚えていますか?
運動方程式は、加速度\(a\)を求めるための方程式です。長々と立式から計算まで扱っていましたが、やっていることは非常に単純な話で、
\(ma=F\) より、\(m\)を移項して、\(a=\displaystyle\frac{F}{m}\)
これだけです。
\(F\)の中身が複雑だったので、難しく感じたと思いますが、やっていることは\(m\)を移項するという一点だけです。
なぜ加速度が必要なのか、それは、加速度さえ求めてしまいさえすれば、等加速度3公式に代入することで、いつ、どこに、どのくらいの速さで運動しているかを全て解析可能となるので、欲しい運動の予測結果を大概は求めることができるからです。
だったら、わざわざ難しい運動方程式を解いてから、等加速度の公式に代入する、なんていう過程を踏まなくても、運動方程式も等加速度公式も、公式のまま先にまとめてしまって、得られた結果を新しい公式としてしまえば、これらの長い長い過程をもっと単純に計算できるんじゃないかと、そういう疑問を先人は持ったわけです。
文章だと分かりにくいですから、実際にちょっとやってみましょうか。
運動方程式
\(ma=F\) より、
加速度は
\(a=\displaystyle\frac{F}{m}\)
これを、等加速度公式
\(v=v_0+at\)
に代入すると、
\(v=v_0+\displaystyle\frac{F}{m}t\)
\(v-v_0=\displaystyle\frac{F}{m}t\)
\(mv-mv_0=Ft\)
となりました。つまり、運動量の変化は、その物体がされた力積と等しいことが分かります。つまり、ある運動量をもつ物体に力積を加えてやると、そのときにした力積分だけ運動量が増える、ということを表していますね。
運動方程式を長々と解いて、等加速度公式に代入しなくても、運動量と力積さえわかってしまえば、運動方程式を解いて等加速度公式に代入したことと同じ結果を即座に求めることができるというわけです。これは非常に便利!
運動量と力積の関係(簡易表記版)
\(\Delta p = I\)
\(\Delta p\):運動量の変化
\(I\):物体に加えた力積
運動量と力積の関係(内容表記版)
\(mv-mv_0=F\Delta t\)
(あとの運動量)-(まえの運動量)=(力積)
運動量と力積の関係(移項した形)
\(mv=mv_0+F\Delta t\)
(あとの運動量)=(まえの運動量)+(力積)
撃力
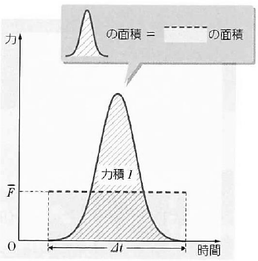
短い時間だけはたらく大きな力のことを、撃力といいます。
向きが一定で大きさが実線のグラフのように変化する力がはたらくとき、力積\(I\)の大きさは、斜線部分の面積で表されます。
これと長方形の面積が等しくなるような力\(\bar{F}\)を考えると、この力が、この時間内での「平均の力」となります。
加える力はベクトル量なので、右向きを正にしたときに仮に左向きの力を考えると、マイナスになります。マイナスの力もありとして力積を考えると、力積もマイナスを取ることがあると分かりますね。
ここでのグラフは一例として正の領域しかない撃力グラフを描きましたが、もちろん、ちょうど上下を逆にしたように、負の面積を示す撃力グラフも存在します。
負の力積グラフに関する問題は、共通テストの試行テストで出題されていますので、どこか機会があるときに見ておくと良いと思いますよ。
