リ物基　応問59

(1)

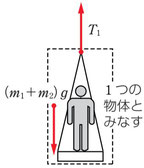
これはさしたる問題もないかと思います。床にいる人が滑車を使って、板に乗っている人を持ち上げますが、このとき、板と人を一つの物体としてまとめてしまえば、質量\(m_1+m_2\)のものを持ち上げていることに相当しますので、

　\(T_1=(m_1+m_2)g　[N]\)

 

です。単位忘れに注意してください。

床と板の間の垂直抗力はどうするんですか？という質問を何人かから受けましたが、図と問題文をよく見てください。板は床から離れて、すでに空中にいますので、垂直抗力はありませんよ。

 

 

(2)

(a)

作図の仕方に気を付けなければいけません。

まずは人にかかる力を作図してみましょう。

 

まず人にかかる重力\(m_1g\)を作図します。これは問題ないですね。

 

次に、人にかかる垂直抗力\(N_2\)を作図します。これも問題ないですね。

 

最後に、張力ですが、これが間違えやすいところです。人はひもにぶら下がることで少し軽くなったように感じます。ということは、人はひもによって上向きに引っぱられているということになります。

 

言葉で考えてみましょう。「人が、ひもを、ひく力」があって、これのイメージは大丈夫だと思います。

この力を言い換えると、「ひもが、人に、ひかれる力」です。ということは、この力は「ひもが、ひかれる力」であって、人は関係ないということです。

 

人がうけるのは、この力の反作用にあたる力ですので、「ひもが、人を、ひく力」と書かれる力が、人にかかっている力、ということになります。よってひもとの接点には上向きの力を作図することになります。

上に力を作図するので、確かに人は軽くなっているように感じてもおかしくはないですよね。

 

さて、難しいのはそこだけでしたね。

よって、人についての力のつり合いの式は、

 

　\(T_2+N_2=m_1g\)

 

となります。ここでは、式を答えよ、とだけ問われていますので、特段、単位をつけて置く必要はありません。あっても問題ないですが、なくていいです。

 

 

(2)

(b)

次に、板についてのつり合いの式を立てます。

 

まず重力\(m_2g\)。これは問題なしですね。

 

次に、人が乗っているために、人が板を押す力が作図されます。これは先ほど書いた垂直抗力\(N_2\)の反作用に相当するので、大きさはおなじ\(N_2\)となります。

 

そして、板の両端がひもで支えられているので、その左右からの張力が斜め向きに働くはずですが、それを考えるとややこしいので、まとめて一番上の、ひもが１本になっているところの張力で代用してしまいます。いま、全体はつりあって静止していますので、これは(a)で与えた\(T_2\)と同じ大きさでなければいけませんね。

 

もし大きさが違えば、滑車がどちらか回りに動き出してしまいます。

 

よって、作図結果は図に示したようになり、板についての力のつり合いの式は

 

　\(T_2=N_2+m_2g\)

 

となりました。