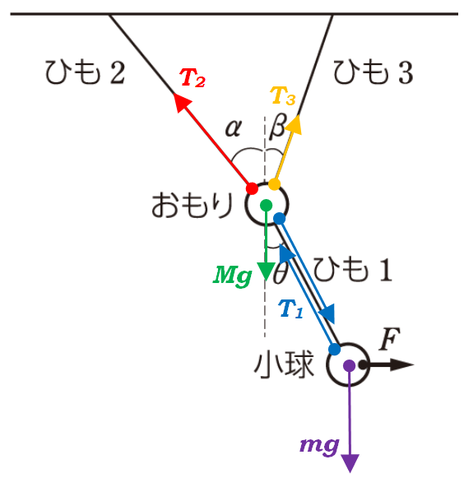
とりあえず、ひもが3本ありますので、3つの張力を作図してしまいます。
それから、物体が2つありますので、それらの重力も作図してしまいましょう。
ひも1は両側からの張力を考えますので、両方からの張力を作図しておきます。
(1)
問題文の誘導に乗っかる形で問題を解いていきましょう。
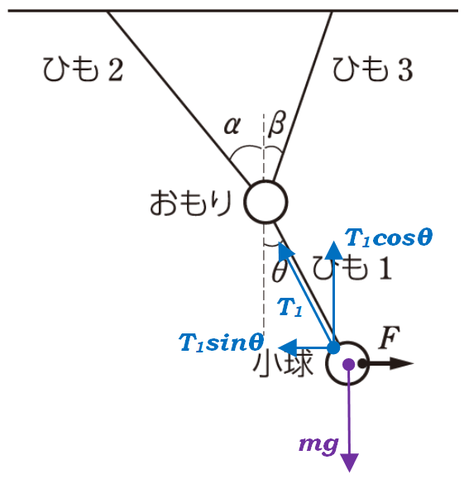
すでに矢印がたくさんで見づらい状態になっていますが、これらの矢印のうち、まずは下についている小球についてだけ考えることにします。
張力を鉛直方向と水平方向に分解すると、力のつり合いの式は、
[水平] \(T_1sin\theta=F\)
[鉛直] \(T_1cos\theta=mg\)
となりました。ここだけであればそんなに難しくなさそうですね。
(2)
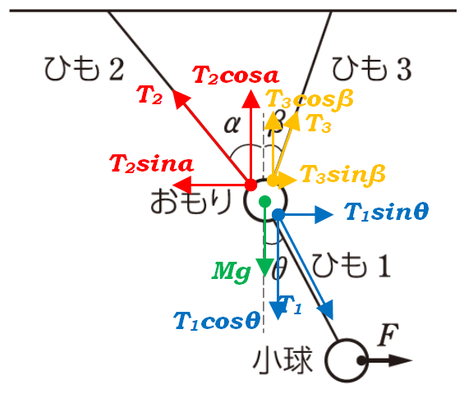
(1)と同じ作業を、今度はおもりの方でもチャレンジしてみます。3つの張力を全て鉛直方向と水平方向に分解します。
このとき、最初に作図してあるはずですが、おもりそのものの重力\(Mg\)の存在を忘れないようにしてください。
図は複雑ですが、見るべき部分は鉛直成分と水平成分だけです。
力のつり合いの式は、
[水平] \(T_2sin\alpha =T_3sin\beta +T_1sin\theta\)
[鉛直] \(T_2cos\alpha +T_3cos\beta =Mg+T_1cos\theta\)
となります。リードの模範解答は「\(=0\)」となるように式がまとめられていますが、水平成分なら「左矢印の和=右矢印の和」、鉛直成分なら「上矢印の和=下矢印の和」という考え方で十分です。
(3)
(1)(2)で書き出した4本の式を連立すると、一応は求まるようにはできていますが、式が複雑なので少しだけ条件を緩めてくれています。
\(F=F_0\)のとき、ひも3がたるむ、つまり\(T_3=0\)となりますよ、という条件にしてくれていますので、4つの式は
(1)[水平] \(T_1sin\theta=F\)
(1)[鉛直] \(T_1cos\theta=mg\)
(2)[水平] \(T_2sin\alpha =T_3sin\beta +T_1sin\theta\)
(2)[鉛直] \(T_2cos\alpha +T_3cos\beta =Mg+T_1cos\theta\)
から
(1)[水平] \(T_1sin\theta=F_0\)
(1)[鉛直] \(T_1cos\theta=mg\)
(2)[水平] \(T_2sin\alpha =T_1sin\theta\)
(2)[鉛直] \(T_2cos\alpha =Mg+T_1cos\theta\)
と変更できます。
ここで(1)で求めた2式はどちらも(2)で求めた式にそのまま代入できますので、代入させてみると、
[水平] \(T_2sin\alpha =F_0\)
[鉛直] \(T_2cos\alpha =Mg+mg\)
となります。ここから、2式を分数の式で1本化してやると、
\(\displaystyle\frac{T_2sin\alpha}{T_2cos\alpha}=\frac{F_0}{(M+m)g}\)
となるので、約分して、
\(tan\alpha=\displaystyle\frac{F_0}{(M+m)g}\)
よって
\(F_0=(M+m)g tan\alpha\)
とまとめることができました。
(4)
(3)の4本の連立式のうち、上の2本だけ取り出して考えます。\(F=F_0\)のとき、\(\theta=\theta_0\)とするそうですので、添え字だけ書き替えて、式をもう一度もってくると、
(1)[水平] \(T_1sin\theta_0=F_0\)
(1)[鉛直] \(T_1cos\theta_0=mg\)
これを先ほどと同様に分数の式で一本化してやると、
\(\displaystyle\frac{T_1sin\theta}{T_1cos\theta}=\frac{F_0}{mg}\)
から、約分して、
\(tan\theta_0=\displaystyle\frac{F_0}{mg}\)
\(mgtan\theta_0=F_0=(M+m)g tan\alpha\)
\(tan\theta_0=\displaystyle\frac{M+m}{m}tan\alpha\)
