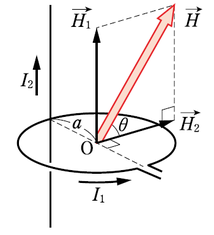
問題文のままの図の視点からだと解きにくいので、少しずらした視点から見ることを考えます。
図は模範解答から取ってきた図です。模範解答でもずらして描いているので、そうするのが大多数なのかもしれませんね。
点\(O\)には、直線電流がつくる磁場と、円形コイルが作る磁場の二つが同時にかかっています。
指針としては、それぞれの磁場を公式通り求めて、図のように三平方の定理を使って重ね合わせてやる、という流れになります。
(1)
直線電流が作る磁場は、
\(H=\displaystyle\frac{I}{2\pi r}\) より
\(H_2=\displaystyle\frac{I_2}{2\pi a}\)
また、円形コイルが作る磁場は、
\(H=\displaystyle\frac{I}{2r}\) より
\(H_1=\displaystyle\frac{I_1}{2a}\)
となります。なので、図のように三平方の定理を使って磁場の合成をしてやると、
\(H=\sqrt{H_1^2+H_2^2}\)
\(H=\sqrt{(\displaystyle\frac{I_1}{2a})^2+(\frac{I_2}{2\pi a})^2}\)
\(H=\sqrt{\displaystyle\frac{I_1^2}{(2a)^2}+\frac{I_2^2}{(2\pi a)^2}}\)
\(H=\displaystyle\frac{1}{2a}\sqrt{I_1^2+\frac{I_2^2}{\pi^2}}\)
となりました。
(2)
\(tan\theta\)も、作図が終了してしまえば大した計算労力はかかりません。
\(tan\theta=\displaystyle\frac{H_1}{H_2}\)
\(=\displaystyle\frac{\frac{I_1}{2a}}{\frac{I_2}{2\pi a}}\)
分子分母に\(2\pi a\)をかけると、
\(tan\theta=\displaystyle\frac{\pi I_1}{I_2}\)
となりました。
