■解答
(あ) \(dsin\theta[m]\) (い) \(2\pi\displaystyle\frac{dsin\theta}{\lambda}[rad]\) (う) \(2\pi m[rad]\)
(え) \(N^2A_0^2\) (お) \(\displaystyle\frac{2\pi n}{N}\) (か) \(\displaystyle\frac{sin^2 \frac{N\delta}{2}}{sin^2\frac{\delta}{2}}A_0^2\)
(き) \(\displaystyle\frac{4}{9\pi^2}\) (く) \(\left(m+ \displaystyle\frac{1}{N} \right) \lambda\) (け) \(\displaystyle\frac{\lambda}{d cos\theta_m}\)
■解説
(あ) \(dsin\theta\) 問題ないでしょう。
(い)
経路差が\(dsin\theta\)ですが、これはイコール光路差が\(dsin\theta\)ということでもあります。
光路差を位相差に直すときには、\(\displaystyle\frac{2\pi}{\lambda}\)をかけてやります。
すると、位相差は、
\(\Delta=\displaystyle\frac{2\pi}{\lambda}dsin\theta\)
となります。
(補足)
光路差を位相差に直すときは、波長一つ分の長さで\(2\pi\)の位相を持つので、比を立ててやると、
\(\lambda:2\pi\) = 光路長:位相 = 光路差:位相差
となることから、
\(\lambda×\)位相差 = \(2\pi×\)光路差
よって
位相差=\(\displaystyle\frac{2\pi}{\lambda}×\)光路差
としてやる換算方法があり、京大入試ではよく見かける手法です。
(う)
強め合いの干渉条件式は
\(dsin\theta=m\lambda\)
なので、(い)の関係式を代入して、
\(\Delta=\displaystyle\frac{2\pi}{\lambda}・m\lambda\)
\(=2\pi m\)
(え)
本文に「光の強度は振幅の2乗に等しいので」とありますので、素直に文章通りを式に直します。
スリット\(N\)個から\(N\)個の波が、それぞれ振幅\(A_0\)で出ていますので、単純に重ね合わせてやると、\(NA_0[m]\)の振幅となります。
ここから「振幅の2乗に等しいので」、
\(K_0=(NA_0)^2\)
\(=N^2A_0^2\)
としてやります。
一般的には、単純に加算はできず、三角関数の合成和を計算しないといけませんが、「明線の位置での光の強度\(K_0\)」を問われているので、位相がどのようにふるまっているかを細かく考えなくても、最大振幅を足し合わせればよい、ということになります。
(お)を解くにあたり、この問題文に何が書いてあるのかを、一旦分かりやすく説明し直してみることにします。
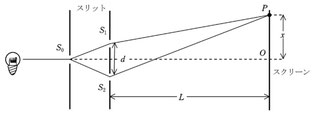
ここでヤングの実験の図を持ってきました。スリットを通過した後の光がスクリーン上の点\(P\)まで届くのに、わずかな経路差が生じるために光が干渉するんでしたよね。
そして、その経路差が位相差として\(0,\pi,2\pi,...\)だけずれていれば光は強め合い、\(0.5\pi,1,5\pi,2.5\pi,...\)だけずれていれば光は弱め合います。
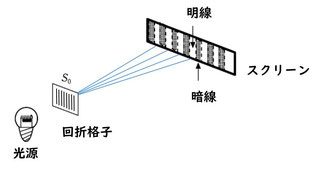
これは回折格子でも同様の説明の仕方になります。スリット間の距離がわずかであるとはいえ、光の波長も負けないくらい十分に小さいですので、スリット1からスクリーン上のある点\(P\)までの距離と、スリット2から点\(P\)までの距離、スリット3から点\(P\)までの距離は、すべて違う値になるはずです。
これらの位相差が\(\pi\)の整数倍か半整数倍かを読めば明線か暗線かがわかりますが、この問題では、より一般的に考えます。
位相差がどのくらいあるかは分からないが、何\(rad\)かの位相差がある、という状況です。
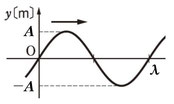
仮に、スリット1からスクリーンに到達した光の波長が図のようであったとします。一般的な状況を考えますので、スクリーンに到達したときにちょうど波の山が来たり谷が来たり、あるいは交点ぴったりでスクリーンに当たるかと言われるとそうではありませんよね。
この図では、位相に換算して50°くらいですかね。\(\lambda\)と書かれた交点を0°とすると、そこから50°くらい進んだところでスクリーンに到達しましたよ、という意味として考えます。
50°としたのは目分量です。何かを計算して出したわけではありません。
この位相のズレを\(A_1\)と表記することにします。
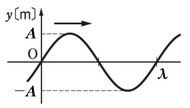
スリット2からスクリーンに到達した光の波長はスリット1から出た光より若干長い経路を通りますので、図のように波の長さが少しだけ長くなります。
この図での位相のズレは、そうですね、目分量ですが80°くらいでしょうかね。この位相を\(A_2\)と表記します。

同様にスリット3からスクリーンに到達した光の位相のズレも考えます。
この図での位相のズレは、110°ということにしましょうか。この位相は\(A_3\)と表記します。
このように、回折格子から出た\(N\)個の光線の位相をそれぞれ書き出して、同じ原点から矢印表記してやると、半径\(A_0\)の円をぐるっとたどる形になります。
問題中にある図2(a)の図の意味はこのような意味になります。
本文の言葉でいう「観測点でのスリット1からの光の波の変位は、図2(a)のように、大きさ\(A_0\)のベクトル\(A_1\)の\(y\)軸への射影に対応し、その位相は\(x\)軸と\(A_1\)とのなす角に対応する」ということです。
ここでは、スリットが\(N\)個ありますので、同じ作業を\(N\)回行った結果、\(A_N\)は170°くらいでおわりました、という図になっています。\(A_i\)が延々とぐるぐる回っているわけではありません。
さて、なぜこのような図を考えているのか、という根本の部分に疑問を持ってみましょう。
今これらスリットから出て行った波を重ね合わせようとすると、本来なら
\(y=A_0sin(\theta+50°)+A_0sin(\theta+80°)+A_0sin(\theta+110°)…\)
のような計算を追わなければいけません。
加法定理を駆使して三角関数表や関数電卓を片手に、力押しもできるかもしれませんが、どう考えても手計算で行うには現実的ではありません。
そこで、位相のズレだけを取り出して、問題文の図2の(a)のように図を描き出しました。また、別の図として、位相差を表す\(A_i\)をベクトル合成する形(矢印が連続して並ぶ形)に描きかえて、図2(b)を作図しました。
この図を作ると、本文の説明から
「重ね合わされた光のベクトル\(A_s=A_1+A_2+...+A_N\)は、図2(b)のように表せ、その強度は\(\left| A_s \right|^2\)で与えられる」
とありますので、ベクトル和の始点と終点だけから光の強度を推測できるようです。
(補足)
ここで少し話がそれますが、数学の公式の一つに、
\(y=Asin\theta+Bcos\theta\)
\(=\sqrt{A^2+B^2}sin(\theta+\alpha)\)
という関係式があるので、合成する三角関数の振幅部分がすべて\(A_0\)なのであれば、
\(y=A_0sin\theta+A_0cos\theta\)
\(=\sqrt{2A_0^2}sin(\theta+\alpha)\)
というようにまとめて、複数の三角関数を一つの三角関数に合成していく方法があります。それに似た作業をしていると思ってもいいかもしれません。
こうして合成して一つの三角関数にしてしまったものの振幅部分を\(A_s\)と表現して、「光の強度は振幅の2乗に等しい」ので、「その強度は\(\left| A_s \right|^2\)で与えられる」と話が続いていくわけです。
(お)
さて、図2(b)を見てみましょう。スリット\(N\)個で、それぞれのスリット間の位相差が\(\delta\)ですので、中心角は\(N\delta\)となります。\(\delta\)の幅は未定ですが、大きさを調整すれば、ベクトルがちょうど1周して多角形を描く図を作ることもできますね。これが本文でいう「重ね合わせられた光の強度\(\left| A_s \right|^2\)が厳密に0となる点」に相当します。
場合によってはちょうど1周と言わず、ちょうど2周かもしれませんし、ちょうど3周かもしれませんが、ぴたっと重ねることはできなくはないです。
このとき、中心角が \(2\pi×\)整数 のとき、
\(\left| A_s \right|=0\)
よって
\(N\delta=2\pi n\)
\(\delta =\displaystyle\frac{2\pi n}{N}\)
(か)
(お)では、\(\left| A_s \right|=0\)の特別な例を取り出して計算をしましたが、一般的にはそうはなりません。そこで、一般的に強め合いも弱め合いもしない点における間の部分の光の強度はどうなっていますか、求めなさい、という問題をここで出題しています。
ただ、その物理的な意味を読み取った上で解答しなさい、というレベルを求めているわけではありませんので、素直に問題文の誘導に乗って解いていきます。
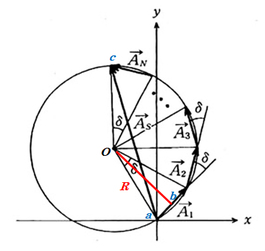
いま、図2(b)のように光のベクトルの始点と終点がすべて同一の円周上にあると考えています。そして、\(N\)個の光の重ね合わせを考えているため、ベクトルの和は、図の\(ac\)に相当し、ここの長さを求めなさい、という問題として出題されています。
これは、未知の半径を\(R\)として、中心角\(N\delta\)となるような三角形\(Oab\)を利用すればよさそうです。半径\(R\)が分かっていれば、余弦定理で求められそうですが、半径\(R\)が未知なので、まずはそちらを求めてやることにします。
点\(O\)から、\(A_1\)に向かって垂線を引き、その垂線の足を\(b\)としておきます。そして、\(△Oab\)で正弦定理を使うと、
\(R\sin\displaystyle\frac{\delta}{2}=\frac{A_0}{2}\)
よって
\(R=\displaystyle\frac{A_0}{2\sin\frac{\delta}{2}}\)
と求まります。これを使って、\(△Oac\)で余弦定理から、
\(A_s^2=R^2+R^2-2R^2\cos N\delta\)
\(=2R^2-2R^2\cos N\delta\)
\(=2R^2(1-\cos N\delta)\)
\(=2・\displaystyle\frac{A_0^2}{4\sin^2\frac{\delta}{2}}(1-\cos N\delta)\)
\(=\displaystyle\frac{1-\cos N\delta}{2\sin^2\frac{\delta}{2}}A_0^2\)
となりました。問題文に指定されたとおり、\(A_0\)、\(\delta\)、\(N\)を用いて表しているので、ここでとめてしまっても正解にはなると思いますが、先のことを考えて、\(\sin\theta\)と\(\cos\theta\)を統一しておきます。
\(\cos2\theta=1-2\sin^2\theta\) であるから、
\(A_s^2=\displaystyle\frac{1-(1-2\sin^2\frac{N\delta}{2})}{2\sin^2\frac{\delta}{2}}A_0^2\)
\(=\displaystyle\frac{2\sin^2\frac{N\delta}{2}}{2\sin^2\frac{\delta}{2}}A_0^2\)
\(=\displaystyle\frac{\sin^2\frac{N\delta}{2}}{\sin^2\frac{\delta}{2}}A_0^2\)
と変形しておきます。ここまでで(か)の答えです。
(き)
図3(a)のピークのすぐ横を拡大した図が(b)です。こっそり軸を移動させてありますが、そこは重要なポイントではありませんのでスルーしておきます。最大ピークのすぐ横に別のピークがいくつかあり、そのうちの一つ目を\(K_1\)としています。
そして、この\(K_1\)は\(\delta_1\)と\(\delta_2\)の中点に限りなく近いところにある、としています。
(お)で、\(\delta_n=\displaystyle\frac{2\pi n}{N}\) を与えているので、そのまま使っていきましょう。
\(\delta_1=\displaystyle\frac{2\pi}{N}\)
\(\delta_2=\displaystyle\frac{4\pi}{N}\)
となりますので、
\(\delta=\displaystyle\frac{\delta_1+\delta_2}{2}=\frac{\frac{2\pi}{N}+\frac{4\pi}{N}}{2}=\frac{3\pi}{2}\)
これを、\(A_s^2\)に適用させてみましょう。
\(A_s^2=\displaystyle\frac{\sin^2\frac{N\delta}{2}}{\sin^2\frac{\delta}{2}}A_0^2\)
\(=\displaystyle\frac{\sin^2\frac{3\pi}{2}}{\sin^2\frac{3\pi}{2N}}A_0^2\)
ここで、\(N\)が非常に大きいということは、分母にある(\displaystyle\frac{3\pi}{2N}\)は非常に小さいということになります。
なので、\(sin\theta≒\theta\) という近似を用いることができます。よって、
\(A_s^2=\displaystyle\frac{\sin^2\frac{3\pi}{2}}{(\frac{3\pi}{2N})^2}A_0^2\)
\(=\left( \displaystyle\frac{2N}{3\pi}\right)^2 \sin^2\frac{3\pi}{2}A_0^2\)
\(=\displaystyle\frac{4N^2}{9\pi^2}A_0^2\)
これが\(K_1\)です。\(K_0\)は、(え)で\(N^2A_0^2\)と求まっていますので、それらの比は、
\(\displaystyle\frac{K_1}{K_0}=\frac{4}{9\pi^2}\)
となります。これはおよそ\(\frac{4}{90}\)ですので、メインの\(K_0\)のピークと比較して、\(K_1\)は、だいぶ小さい高さのピークになるようですね。
(く)
\(m\)次の明線が見られるとき、スリット間の経路差は\(d\sin\theta_m\)となります。ただ、この問題では経路差は問われておらず、位相差ベースで話が進んでいますので、経路差はまとめて\(l\)としておいて、かわりに位相差を表現することにします。この換算方法は、(い)の説明の続きにある補足を読んでみてください。
位相差は \(\displaystyle\frac{2\pi}{\lambda}l\) となります。そしてこれを、\(\Delta_m\)と書くことにしています。
さらに本文を読み進めると、\(m\)次の明線のすぐ横の暗線について同様に考えると、スリット間の経路差は\(d\sin\theta'_m\)となり、位相差が\(\delta_1\)だけ増えていると読み取れます。このときの経路差をまとめて\(l'\)としてしまって、同じく位相差を表現すると、
位相差は \(\displaystyle\frac{2\pi}{\lambda}l’\) となり、これを、\(\Delta_m+\delta_1\)と書くことにしています。
さて、\(l'\)を求めてみましょう。
\(\displaystyle\frac{2\pi}{\lambda}l’=\Delta_m+\delta_1\)
\(\displaystyle\frac{2\pi}{\lambda}l’=2\pi m +\displaystyle\frac{2\pi}{N}\)
\(\displaystyle\frac{2\pi}{\lambda}l’=2\pi \left( m +\displaystyle\frac{1}{N} \right)\)
よって
\(l'=\lambda\left( m +\displaystyle\frac{1}{N} \right)\)
(け)
\(N \rightarrow\)大 なら、\(\beta_m \ll 1\) となり、\(\beta_m=\displaystyle\frac{b_m}{N}\)
⇒ \(b_m\)を\(d,\lambda,\theta\)を用いて表す。
\(l'=d\sin(\theta_m+\beta_m)\)
\(=d(\sin \theta_m \cos\beta_m +\cos\theta_m \sin\beta_m)\)
\(≒d(\sin\theta_m+\beta_m \cos\theta_m)\) ―――①
(く)より \(l'=\lambda\left( m +\displaystyle\frac{1}{N} \right)\) ―――②
①②より、
\(d\sin \theta_m+d\beta_m \cos\theta_m=\lambda\left( m +\displaystyle\frac{1}{N} \right)\)
\(d\sin\theta_m +d・\displaystyle\frac{b_m}{N}\cos\theta_m=\lambda\left( m +\displaystyle\frac{1}{N} \right)\)
ここで左辺第一項の\(d\sin\theta_m\)は、\(=l=m\lambda\)であるので、
\(d・\displaystyle\frac{b_m}{N}\cos\theta_m=\lambda\displaystyle\frac{\lambda}{N}\)
\(d・b_m\cos\theta_m=\lambda\)
\(b_m=\displaystyle\frac{\lambda}{d\cos\theta_m}\)
