算術平均
実験をすると、測定値が得られます。ですが、どれだけ精密に測定したとしても、測定するごとに誤差が出てしまうために、毎回違う結果となってしまいます。
これをどのように結果としてまとめていくといいのでしょうか。
手っ取り早い方法として、平均をとる、という作戦が考えられますね。
小学校の算数以来、何回も計算したことがあるでしょうから、とても計算には慣れていると思います。
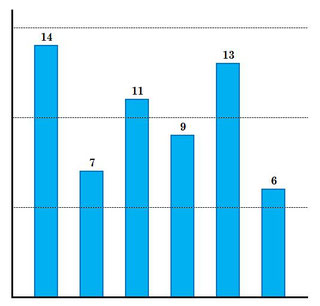
仮に、何かを測定したときの結果が図のようになったとします。この6回分の測定の結果の平均を出そうと思ったら、すべての値を足し合わせて、6で割ってやるといいですね。
\(14+7+11+9+13+6=60\)
\(60÷6=10\)
となり、平均値は\(10\)と求まります。
このように、測定値を全て足し合わせたあとに、測定回数で割り算して求める平均のことを「算術平均」と言います。
このとき、測定した値を\(x_i(=x_1,x_2,x_3...)\)として、算術平均を\(\langle x \rangle\)と書くことにします。
測定した回数を\(n\)とすると、算術平均は
\(\langle x \rangle=\displaystyle\frac{x_1+x_2+...+x_n}{n}\)
と書くことができます。
さらに、\(x_i\)をすべて足し合わせる、という記号として、シグマ(\(\Sigma)\)を使うと、
\(\langle x \rangle=\displaystyle\frac{\Sigma x_i}{n}\)
と書くこともできます。通常数学では、シグマ(\(\Sigma)\))の上下には、いくらからいくらまで足し合わせるのかを明記する必要がありますが、ここでは「全部足すときは上下の添字を省略する」というルールでいこうと思います。何も書いていなければ、全部足すことなんだなあと思ってください。
▼算術平均
\(\langle x \rangle=\displaystyle\frac{x_1+x_2+...+x_n}{n}\)
\(=\displaystyle\frac{\Sigma x_i}{n}\)
偏差と分散

さて、いま平均が\(10\)と判明しましたが、実際の測定値には一つも\(10\)が含まれていません。\(10\)付近にあることは分かりましたが、数値は平均からぶれていますね。
このとき、各測定値が平均からどのくらいずれているか、言い換えると、「平均値と測定値の差」のことを「偏差」と言います。
模試を受ける人たちの中には、よく、「偏差が\(60\)だった」とか、「偏差が\(5\)あがった」とかいう表現を使う人を見ますが、これは「偏差値」と「偏差」の違いをごちゃまぜにしています。
仮に平均点が\(50\)点のテストがあったとすると、「偏差が\(60\)だった」生徒は、\(110\)点か、あるいはマイナス\(10\)点を取ったことになりますし、得点が\(45\)点だった人の「偏差が\(5\)あがった」とすると、平均との差があがる、つまり平均点から離れる意味になり、得点は\(40\)点となって、より一層平均点から遠のいてしまうことになりますね。
「偏差」と「偏差値」は別の用語です。偏差値教育に染まって生活しているうちは、(概念自体は、便利は便利なので)知っておくといいと思います。
さて、測定値が平均からプラスマイナスでどのくらい離れているかを調べるために、図のようにそれぞれの測定値の偏差を書き出してみました。これの平均(算術平均)を計算してやると、プラスマイナスいくらになるのか求まりそうですね。
ところが、少し手を動かしてみるとすぐに気づきます。偏差の平均は\(0\)になってしまいます。それはそのはずですね。平均はそもそも測定値の「真ん中」の値ですから、ずれを合計したところで「真ん中」に行きつくに決まってます。
▼偏差
測定値と平均値の差のこと。偏差の平均は常にゼロになる。
\(\Delta x=x_i-\langle x \rangle\)
偏差の平均を出したいですが、偏差にプラスの値とマイナスの値があるのが邪魔ですね。
そこで、それぞれの偏差を\(2\)乗してやることにしましょう。するとすべて正の数になります。
平均から多いか少ないかを場合分けすることなく、平均から離れていれば大きい値、平均に近ければ小さな値を取ることになります。
これの平均(算術平均)を取ることにしましょう。
すると、
\(16+9+1+1+9+16=52\)
\(52÷6=8.666666...\)
となりました。つまり、\(8.7\)ほどの値が平均値からの離れ具合を表す量になる、ということです。
この値を「分散」といい、数字が大きければそれぞれの測定値は平均から散らばっていることを表していて、数字が小さければ複数回の測定はそれぞれ平均に近い値を出していた、ということを表します。
分散を \(\sigma^2\) と表すことにします。
▼分散
偏差を2乗したものの平均。小さいほど、測定値の散らばり方が小さい。
\(\sigma^2=\displaystyle\frac{\Sigma(\Delta x)^2}{n}\)
\(=\displaystyle\frac{\Sigma(x_i-\langle x \rangle)^2}{n}\)
標準偏差
偏差の符号を取りはらう意図から、分散を求めてみました。
ところが、これを、測定値と平均値とのずれ、というには正確さがありませんね。
全体として、測定値がどの程度バラついているのかはうっすらと分かりましたが、そもそも偏差を2乗してしまっているので、値としてはあまり信じられません。
より感覚と一致するように調整してやるとすれば、シンプルに分散の平方根をとってやりましょう。
もともと偏差を2乗したところから計算をスタートしたので、分散にルートをとって、だいたい元と同じくらいの数字になるように直してやりましょう、ということです。
すると、
\(\sqrt{8.6666....}=2.9439...≒2.9\)
となりました。つまり、今回の測定値は\(10\pm2.9\)くらいだ、ということになりますね。
有効数字などの細かい表記のルールは今は置いておくとして、数字の部分だけ見ると、あながち間違ってはなさそうです。
グラフを見る限り、だいたい平均\(\pm3\)くらいのあたりだと言ってもよさそうですね。
こうして出した値を「標準偏差」といい、物理実験では、これが「実験誤差」に相当するものになります。
▼標準偏差
分散の平方根をとったもの。物理実験でいう実験誤差に相当する。
\(\sigma=\sqrt{\displaystyle\frac{\Sigma(\Delta x)^2}{n}}\)
\(=\sqrt{\displaystyle\frac{\Sigma(x_i-\langle x \rangle)^2}{n}}\)
数式だけをひろって読むと、ちょっと難しいかもしれませんが、本文をたどってもらうと、全然たいしたことをやっていないことに気付くと思います。数式は所詮数式です。式の難しさに飲み込まれないように、考え方の部分を習得してもらえればと思います。
