(1)
最初に、ばねの伸び\(x\)がどのくらいなのかを求め、それをフックの法則\(F=kx\)に代入することで弾性力の大きさを求める、という方向で解いていくのを目指しましょう。
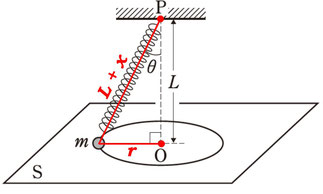
ばねの自然長は\(L\)です。それを回転させると、回転の影響を受けてばねがのばされ、いくらか伸びます。このとき伸びた長さを\(x\)とすると、伸びたばねの全長は\(L+x\)になります。
図のように、回転半径を\(r\)として、値を書きいれましょう。
いま、\(x\)を求めたいので、\(x\)が当然未知数ですが、回転半径の\(r\)も未知数です。
なので、半径の部分を使わずに\(x\)についての式を立てると、
\((L+x)\cos\theta=L\)
とするのがいいかと思います。これを変形して\(x\)について整理すると、
\(L\cos\theta+x\cos\theta=L\)
\(x\cos\theta=L-L\cos\theta\)
\(x\cos\theta=L(1-\cos\theta)\)
\(x=\displaystyle\frac{L(1-\cos\theta)}{\cos\theta}\)
よって、フックの法則より、今求めたい弾性力は
\(F=kx=\displaystyle\frac{kL(1-\cos\theta)}{\cos\theta}\)
(2)
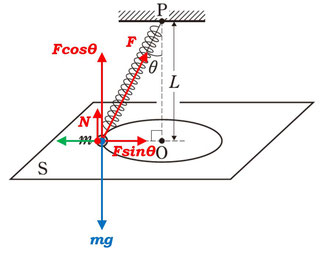
小球にはたらく力を作図します。まず重力。次に弾性力。弾性力は分解までしておきましょう。そして、面と接したまま回転させていますので、垂直抗力がいります。
あとは、解法によりけりですけど、小球と一緒に回転する系で解こうと思いますので、遠心力も作図しておきます。
そして、鉛直方向と、水平方向のそれぞれに力のつり合いの式を立てましょう。
[鉛直]
\(F\cos\theta+N\)\(=\)\(mg\)
\(F\cos\theta\)\(=\)\(mg\)\(-\)\(N\)
[水平]
\(m\displaystyle\frac{v^2}{r}\)\(=\)\(F\sin\theta\)
回転半径\(r\)は自分で置いた文字ですので、解答には使えません。(1)で使った図をもう一度利用して、
\(\tan\theta=\frac{r}{L}\) より
\(r=L\tan\theta\)
これを代入して、
\(m\displaystyle\frac{v^2}{L\tan\theta}\)\(=\)\(F\sin\theta\)
これで(ア)(イ)とも書き出すことができました。
(3)
さて、連立式を解いていきましょう。
\(v\)を求める問題ですので、水平方向の式をスタートに使うことにします。
\(F\sin\theta=\displaystyle\frac{mv^2}{L\tan\theta}\)
\(v^2=F\sin\theta・\displaystyle\frac{L\tan\theta}{m}\)
\(=\displaystyle\frac{kL(1-\cos\theta)}{\cos\theta}・\sin\theta・\frac{L\tan\theta}{m}\)
\(=kL(1-\cos\theta)\tan\theta・\displaystyle\frac{L\tan\theta}{m}\)
\(=\displaystyle\frac{kL^2\tan^2\theta(1-\cos\theta)}{m}\)
\(v=L\tan\theta\sqrt{\displaystyle\frac{k}{m}(1-\cos\theta)}\)
(4)
\(N=0\)のとき、\(\omega=\omega_0\)となります。
水平方向の式は、遠心力を\(m\displaystyle\frac{v^2}{r}\)ではなく、\(mr\omega^2\)として立式しなおしておきます。
(3)で立式した、鉛直方向と、水平方向のそれぞれの式を見比べながら書き出す方がミスが減るかと思います。
[鉛直] \(F\cos\theta=mg\)
[水平] \(mr\omega_0^2=F\sin\theta\)
水平方向の式から、\(r\)を代入して、
\(F\sin\theta=mL\omega_0^2\tan\theta\)
これと、鉛直方向の式
\(F\cos\theta=mg\)
を丸ごと分数化してしまって解くと早く解けそうです。
\(\displaystyle\frac{F\sin\theta}{F\cos\theta}=\frac{mL\omega_0^2\tan\theta}{mg}\)
\(\tan\theta=\displaystyle\frac{L\omega_0^2}{g}\tan\theta\)
\(1=\displaystyle\frac{L\omega_0^2}{g}\)
\(\omega_0^2=\displaystyle\frac{L}{g}\)
\(\omega_0=\sqrt{\displaystyle\frac{L}{g}}\)
