ヤングの実験と実験装置
光の波長はとても短いので、音波のようには明確に回折の現象を見ることができません。ですが、紙に細い切り込みを入れたものを用意して、そこに光を通すと、きちんと回折の現象を見ることができます。
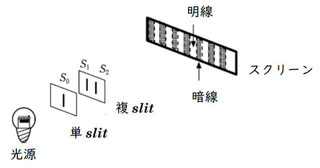
図のように、スリット(すき間)がある遮蔽版を2枚おいて、単色光源を置くと、スクリーンに明暗の縞模様が見えます。
この実験をヤングの実験と言います。1805年頃の実験ですね。
2つの光源を置くと、光が干渉して腹線と節線ができます。これによってスクリーンに明暗の模様ができるわけですが、なぜ豆電球を2つ置いたときには縞模様が見えないのでしょうか。
それは、2つの光源から出る光は必ずしも同位相で出ているとは限らず、しかも振幅も波長も同じとは限らず、ランダムな出方をしているからです。なので、1本のスリットが入った単スリットを置いておいて、その先にさらに2本のスリットが入った板を置いておくことで\(S_0S_1\)と\(S_0S_2\)が等しくなるように設定してやれば、完全に同じ波が完全に同位相の状態で2つの光源としてはたらいてくれますので、こういう装置の設定にしてあるんですね。
ヤングの実験の干渉原理

装置を上から見てみましょう。すると図のようになります。
\(S_0S_1\)と\(S_0S_2\)が等しくなるように設定することで、\(S_1\)と\(S_2\)が光源のような位置づけとなって、この2つの光源から出る光が干渉して、スクリーンに明暗の模様を映し出すわけです。
ちょっとここで、\(S_1P\)と\(S_2P\)の距離について考えてみましょう。スクリーン上の点\(P\)で、光が強め合っているのか、弱め合っているのかを調べたくなったとします。
調べたくない? だめです。今、調べたくなってください。はい。なりましたね。

\(S_1P\)の長さが、ちょうど波長\(10\)個分、\(10\lambda\)だったとしましょう。
そして、\(S_2P\)の長さが、波長\(10.5\)個分、\(10.5\lambda\)だったとします。
すると、\(S_1\)と\(S_2\)からは同位相の波が出ていますので、点\(P\)に付くころには\(S_1\)からの波は谷が到達するのに対して、\(S_2\)からの波は山が到達してしまいます。
お互いの波がちょうど逆向きになっていますので、波は打ち消しあって消えます。つまり、点\(P\)は暗線だということになります。
もし\(S_2\)から\(P\)までの長さが\(11\lambda\)とか、\(12\lambda\)とかであれば、\(S_1\)からくる波と同期して強め合ってくれたんですけどね。残念でした。
もしくは、\(S_1\)から\(P\)までの長さが\(9.5\lambda\)とか、\(8.5\lambda\)とかでも良かったですね。
2つの波が同調するためには、\(S_1P\)と\(S_2P\)の長さの差が、\(\lambda\)の整数倍であってくれさえいればいいわけです。
それが、波の干渉条件のルールでしたよね。
▼(復習)波の干渉条件
2つの同位相源から発生する波について
(経路差) \(=m\lambda\) \((m=0,1,2...)\) 強め合う
(経路差) \(=\left(m+\frac{1}{2}\right)\lambda\) \((m=0,1,2...)\) 弱め合う

今回、その干渉の条件の左辺をより詳しく見ていこうと思います。
波の干渉の単元を学習したときには、単純に経路差、としていましたが、今回、ヤングの実験では経路差は単純な引き算で出すにはちょっと難しそうです。
どうやって経路差を計算するのか、式を追ってみましょう。
まず、図のように、\(S_1\)と\(S_2\)からスクリーンに垂線を引いて、直角三角形を二つ作ります。
この直角三角形のそれぞれで、三平方の定理を適用しましょう。
\(S_1P^2=L^2+\left(x-\displaystyle\frac{d}{2}\right)^2\)
\(S_1P=\sqrt{L^2+\left(x-\displaystyle\frac{d}{2}\right)^2}\)
\(S_2P^2=L^2+\left(x+\displaystyle\frac{d}{2}\right)^2\)
\(S_2P=\sqrt{L^2+\left(x+\displaystyle\frac{d}{2}\right)^2}\)
これらを引き算すると、
\(S_2P-S_1P= \sqrt{L^2+\left(x+\displaystyle\frac{d}{2}\right)^2}-\sqrt{L^2+\left(x-\displaystyle\frac{d}{2}\right)^2}\)
ここで、近似を使うために、\(L\)をくくります。
\(S_2P-S_1P= L\sqrt{1+\displaystyle\frac{\left(x+\frac{d}{2}\right)^2}{L^2}}-L\sqrt{1+\displaystyle\frac{\left(x-\frac{d}{2}\right)^2}{L^2}}\)
\(S_2P-S_1P= L\left[1+\displaystyle\frac{\left(x+\frac{d}{2}\right)^2}{L^2}\right]^{\frac{1}{2}}-L\left[1+\displaystyle\frac{\left(x-\frac{d}{2}\right)^2}{L^2}\right]^{\frac{1}{2}}\)
\(x\)が十分小さいとき、\((1+x)^n=1+nx\)と近似できます。これを使いましょう。
\(S_2P-S_1P= L\left[1+\displaystyle\frac{\left(x+\frac{d}{2}\right)^2}{2L^2}\right]-L\left[1+\displaystyle\frac{\left(x-\frac{d}{2}\right)^2}{2L^2}\right]\)
\(S_2P-S_1P= L+\displaystyle\frac{\left(x+\frac{d}{2}\right)^2}{2L}-L-\displaystyle\frac{\left(x-\frac{d}{2}\right)^2}{2L}\)
\(S_2P-S_1P= \displaystyle\frac{\left(x+\frac{d}{2}\right)^2}{2L}-\displaystyle\frac{\left(x-\frac{d}{2}\right)^2}{2L}\)
\(S_2P-S_1P= \displaystyle\frac{1}{2L}\left(x+\frac{d}{2}\right)^2-\displaystyle\frac{1}{2L}\left(x-\frac{d}{2}\right)^2\)
\(S_2P-S_1P= \displaystyle\frac{1}{2L}\left(x^2+xd+\frac{d^2}{4}\right)-\frac{1}{2L}\left(x^2-xd+\frac{d^2}{4}\right)\)
\(S_2P-S_1P= \displaystyle\frac{x^2}{2L}+\frac{xd}{2L}+\frac{d^2}{8L}-\frac{x^2}{2L}+\frac{xd}{2L}-\frac{d^2}{8L}\)
\(S_2P-S_1P= \displaystyle\frac{xd}{L}\)
はい。ということで、長い計算の末、経路差は \(S_2P-S_1P= \displaystyle\frac{dx}{L}\) となりました。
これが干渉条件の左辺の部分に相当するわけです。
計算過程は少し発展的な内容ですので、初学者には難しいかもしれません。
まずは、左辺が\(\displaystyle\frac{dx}{L}\)になる、ということを、途中過程なしで、なるものはなる、と割り切ってしまって、暗記対応で学習を進めても問題ないと思います。
その後、必要性が出たときに、この左辺の導出について式を追いかけて、原理としてどんなことが考えられているかに立ち返る方がいいでしょう。干渉分野の全体像が見えてきてから始めて、枝葉の部分の知識がスッと入ってくるものです。
▼ヤングの実験の干渉条件
\(\displaystyle\frac{dx}{L}\) \(=m\lambda\) \((m=0,1,2...)\) 明線条件
\(\displaystyle\frac{dx}{L}\) \(=\left(m+\frac{1}{2}\right)\lambda\) \((m=0,1,2...)\) 暗線条件
