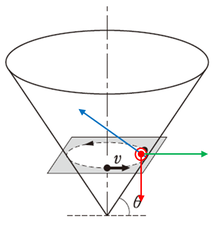
この問題は作図の仕方がキーポイントになります。
物体に重力が加わりますが、その作図をしたあとに、すぐに斜面上に物体があるからと言って、斜面に平行な軸と、斜面に垂直な軸の方向に力を分解する人がいます。
もちろんそれでも解けますが、そのあと遠心力を作図すると、それも斜面に平行な方向と斜面に垂直な方向に分解しないといけなくなり、\(\sin\theta\)と\(\cos\theta\)が2つずつ現れそうなことが目に見えて分かります。
それにともなって、おそらく計算過程も大変になりそうなことが想像されます。
そこで、この問題では、力の分解をする前に、まず最初に作図の矢印を描き切るところからスタートしましょう。
この問題に限った話ではありませんが、どの向きに力を分解したらラクになるのか、という判断は、全部の力を作図しきってから全体を眺めて、そこから判断した方がいいでしょう。
この問題の場合、重力、遠心力、垂直抗力の3力を作図すると、縦軸と横軸を見たまんまに取って、垂直抗力が斜めの力だと解釈すると、分解する力の数は少なくて済みそうです。
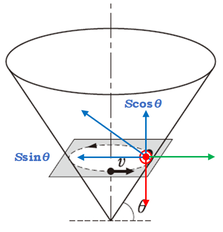
さて、そういうわけで、図のように垂直抗力を分解します。
あとはつり合いの式を立てましょう。
物体とともに運動する系で考えて、垂直抗力を\(S\)とすると、
[水平方向] \(S\sin\theta=m\displaystyle\frac{v^2}{r}\)
[鉛直方向] \(S\cos\theta=mg\)
水平方向の式と鉛直方向の式をそのまま分数にすると、
\(\displaystyle\frac{S\sin\theta}{S\cos\theta}=\frac{m\frac{v^2}{r}}{mg}\)
\(\tan\theta=\displaystyle\frac{v^2}{gr}\)
\(v^2=gr\tan\theta\)
\(v=\sqrt{gr\tan\theta}\)
(2)
周期の公式から、
\(T=\displaystyle\frac{2\pi r}{v}\)
\(T=\displaystyle\frac{2\pi r}{\sqrt{gr\tan\theta}}\)
ここで終わってもいいですが、\(r\)は有理化して1文字にまとめておくと、見た目は綺麗です。
\(T=2\pi\sqrt{\displaystyle\frac{r}{g\tan\theta}}\)
(3)
周期の公式\(T=\displaystyle\frac{2\pi r}{v}\)だけを見て、速さが2倍だから周期は\(\displaystyle\frac{1}{2}\)倍、とするのは判断が早すぎます。
(1)の解答で、\(v=\sqrt{gr\tan\theta}\) とありますので、速さが変わると、円の半径も変わります。
より速く回すことで半径も大きくなる、つまり小球は斜面をはい上がって、少し上の方で回ることになります。
その位置で、1周の時間がどうなっていますか、と問われていますので、パッとは判断できなくなると思います。遠心力の大きさも変わりますね。
きちんと式を追っていきましょう。
(1)より、速さが2倍のとき、軌道半径は4倍。
よって(2)より、周期の式は、分子が4倍、分母が2倍となりますので、全体の値としては2倍、となるわけです。
