(1)
点\(A\)と点\(P\)で、力学的エネルギー保存則を使います。
まず点\(P\)から横に補助線を引いて、点\(P\)が床からどのくらいの高さにあるのかを調べてみましょう。
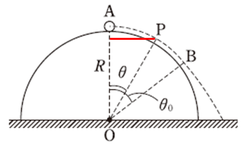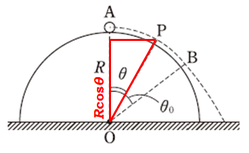
図のように直角三角形を作ると、点\(P\)の高さは\(R\cos\theta\)とわかります。
使ってる図がリードとちょっと違いますが、点\(A\)では右向きに初速度\(v_0\)で動いています。
力学的エネルギー保存則より、点\(P\)での速さを\(v\)とすると、
\(mgR+\displaystyle\frac{1}{2}mv_0^2=mgR\cos\theta+\frac{1}{2}mv^2\)
\(2gR+v_0^2=2gR\cos\theta+v^2\)
\(v^2=v_0^2+2gR-2gR\cos\theta\)
\(v^2=v_0^2+2gR(1-\cos\theta)\)
\(v=\sqrt{v_0^2+2gR(1-\cos\theta)}\)
(2)
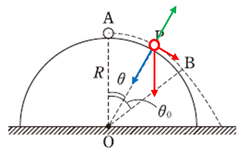
点\(P\)で、小球にはたらく力を作図してみました。重力を作図して、接線方向と、面に垂直な方向に分解します。それから、小球とともに動く系から見たとすると、遠心力が円軌道の外向きに働きますね。あっと、肝心の垂直抗力を作図し忘れてますね。書き足しておいてください。
動径方向(円の半径の方向)で力のつり合いの式を立てると、
\(m\displaystyle\frac{v^2}{R}+N\)\(=\)\(mg\cos\theta\)
\(N=mg\cos\theta-m\displaystyle\frac{v^2}{R}\)
\(N=mg\cos\theta-m\displaystyle\frac{v_0^2+2gR(1-\cos\theta)}{R}\)
\(N=mg\cos\theta-2mg+2mg\cos\theta-m\displaystyle\frac{v_0^2}{R}\)
\(N=(3mg\cos\theta-2mg)-m\displaystyle\frac{v_0^2}{R}\)
\(N=(3\cos\theta-2)mg-m\displaystyle\frac{v_0^2}{R}\)
(3)
点\(A\)ですぐに小球から離れるということは、\(\theta=0\)のとき、\(N=0\)となればいいので、(2)から、
\(0=(3-2)mg-m\displaystyle\frac{v_0^2}{R}\)
\(m\displaystyle\frac{v_0^2}{R}=mg\)
\(v_0^2=gR\)
\(v_0=\sqrt{gR}\)
