記録データの処理については手順のようなものがあります。
①変位\(Δx[m]\)を求める
②平均速\(\bar{v}[m/s]\)を求める
③速度変化\(Δv[m/s]\)を求める
④平均加速\(\bar{a}[m/s^2]\)を求める
という手順で表をまとめていくことをルール化しておくといいでしょう。
少し詳しく書きます
①変位\(Δx=x_2-x_1\)より、2つの区間の差を求めます。
②平均の速度\(\bar{v}\)は、\(Δx\)だけ移動するのに\(Δt\)の時間がかかるということから、
\(\bar{v}=\displaystyle\frac{Δx}{Δt}\) から求めます。
③速度の変化は①と同様の手法で\(\bar{v}\)の差を求めましょう。
④平均の加速度\(\bar{a}\)は、\(Δv\)だけ速度が変化するのに\(Δt\)の時間がかかるということから、
\(\bar{a}=\displaystyle\frac{Δv}{Δt}\) から求めます。
もし、問題の単位が[cm]で出題されていれば[m]に直す操作も追加で必要です。この問題では不要ですね。

さて本題です。
この問題では、①②の作業ができるような表が与えられていますが、実は③④の操作をするための表は省略されています。なので、表を少しだけ書き足してやる必要があります。
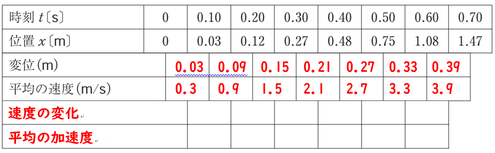
①変位(位置の変化)の欄を埋めるのは単純な話で、隣り合う位置の差を計算してやればいいですね。
②平均の速度は、この問題の場合であれば、変位が\(0.1s\)間での位置の変化を表すことになるので、距離÷時間より、変位の表をちょうど10倍した値が入ることになりますね。

③同様に、平均の速度どうしの間でどのくらいの差があるかを計算して欄に書き足す
④この実験は欄が\(0.1s\)ごとの変化なので、加速度=速度÷時間の関係から、\(0.1s\)を割り算、つまり10倍した値を平均の加速度の欄に書き足す。
(補足)平均の速度の欄の値の意味は、\(0.05s\)で速度\(0.3m/s\)、\(0.15s\)で速度\(0.9m/s\)、\(0.25s\)で速度\(1.5m/s\)という意味になるので、間隔は\(0.1s\)間です。
という手順になります。
リードの模範解答では、グラフを描き、グラフから読み取る問題として扱われているので、解答が分かりにくいという人のために、あえて別解として紹介しておきます。
さて、まとめましょう。
(1)
上の表のとおりです。
(2)
\(0s\)から\(0.10s\)までの平均の速度が\(0.3m/s\)ということをグラフ上で表すときは、\(0.05s\)のときに\(0.3m/s\)であると解釈します。以下同様に\(0.15s\)、\(0.25s\)と点を取ってやってグラフを描いてください。完成図は省略します。手元の教材を確認してください。
(3)
上の表より、平均の加速度がずっと\(6.0m/s^2\)なので、平均とか瞬間とか区別することなく、加速度は\(6.0m/s^2\)と解釈できます。
(4)
\(v=v_0+at\) より
\(v_0=0\)、\(a=6.0\)、\(t=0.50\) なので
\(v = 0 + 6.0×0.50\)
\(v = 3.0m/s\)
とする方が楽かもしれませんね。リードの解答どおり、もちろんグラフから読んでやっても求まります。
