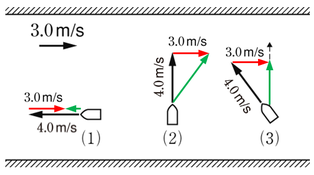
(1)
船が\(4.0m/s\)で上流に進んでも、川の流れで\(3.0m/s\)だけ押し戻されてしまいます。
よって、\(4.0-3.0=1.0[m/s]\)
(2)
船が岸に垂直に\(4.0m/s\)で進み、川によって流されると、岸から見た人は、図の緑色の矢印の方向に進んでいるように見えます。
これを三平方の定理で計算すると、
\(\sqrt{4.0^2+3.0^2}=5.0[m/s]\)
(3)
川によって流されることが分かりましたので、船のへさきを少しだけ上流の方に向けておきましょう。すると川によって流されて、岸から垂直に川を横断するような渡り方に調節することができます。
このとき、同じく三平方の定理より、求めたい速さを\(V\)として、
\(4.0^2=3.0^2+V^2\)
\(16=9.0+V^2\)
\(V^2=7\)
\(V=\sqrt{7}=2.6[m/s]\)
