(1)
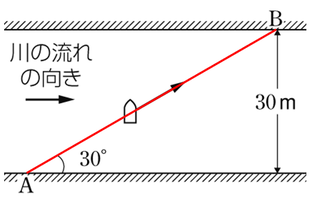
川幅が\(30m\)、船の進行方向が、岸に対して\(30°\)なので、図のように線を並べてやると、大きく\(1:2:\sqrt{3}\)の直角三角形が出来ていることが分かります。
川幅が\(30m\)ということから、船が川を渡る軌跡は\(60m\)であることがわかります。この間を\(15s\)で渡り切るということですから、距離÷時間を計算すれば、
\(v=\displaystyle\frac{x}{t}\)
\(v=\displaystyle\frac{60[m]}{15[s]}\)
\(v=4.0[m/s]\)
(2)(3)
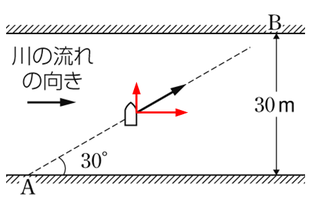
船の速度を縦と横に分解してみます。速度の矢印のつけ根を原点として見たときに、矢印の先の座標がどうなっているか、という部分を見てやると比較的分かりやすいかと思います。
分解すると、図のようになります。
これも\(1:2:\sqrt{3}\)の直角三角形となりますので、斜辺が\(4.0m/s\)であれば、縦が\(2.0m/s\)、横は\(2.0\sqrt{3}[m/s]\)となります。
よって、
(2) \(v_1=2.0[m/s]\)
(3) \(v_2=2.0\sqrt{3}=2.0×1.73≒3.5[m/s]\)
結局、船は岸に垂直に\(2.0m/s\)で進んでいるだけですけれども、川の流れが\(2\sqrt{3}[m/s]\)の速さで流れているために、船が流されて、軌跡は斜め向きになっている、ということを意味しています。
