(1)
水平投射では、鉛直方向には初速度を持たないので、投げてから何秒後に海面に落下するかは、単に自由落下として考えたときに高さ\(40m\)を何秒で落下すればいいのかを求めればよい問題です。
鉛直下向きを正とすると、
\(y=\displaystyle\frac{1}{2}gt^2\) より
\(40=\displaystyle\frac{1}{2}×9.8×t^2\)
\(40=4.9t^2\)
\(400=49t^2\)
\(t^2=\displaystyle\frac{400}{49}\)
\(t=\displaystyle\frac{20}{7}\)
\(t=2.857...≒2.8s\)
(2)
水平方向には落下しませんので、水平方向のみを考えるときは等速直線運動として考えます。
\(x=vt\) より
\(x=21×\displaystyle\frac{20}{7}\)
\(x=3×20=60[m]\)
前問で求まっている\(t\)を代入するときは、四捨五入した\(t=2.8\)でも、扱いにくい\(t=2.857...\)でもなく、もう一つ前の分数の形での代入をすると、厳密な計算ができます。見ての通り、”約”\(60m\)なのではなく、”厳密に”\(60m\)となるようですね。
(3)
小石が海面に落下するとき、斜めに落下してきますが、水平投射の運動の解析は鉛直方向と水平方向に分けて考えます。
この問題では、そのうち、鉛直方向だけの速度成分を求めてください、という問題なので、自由落下の速度公式から計算することにしましょう。
\(v_y=gt\) より
\(v_y=9.8×\displaystyle\frac{20}{7}\)
\(v_y=1.4×20=28m/s\)
(4)
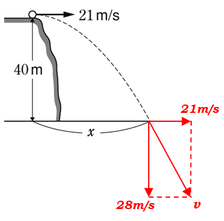
落下する直前、小石の水平方向の速度は\(21m/s\)、鉛直方向の速度は\(28m/s\)であると求まりました。
なので、これらを合わせた速度は、図のように、三平方の定理を使って計算してしまいましょう。
\(v^2=21^2+28^2\)
ここで、正直にかけ算を計算してしまうのではなく、逆に、素因数分解で\(21\)と\(28\)を崩してやります。すると、
\(v^2=(3×7)^2+(4×7)^2\)
\(v^2=3^2×7^2+4^2×7^2\)
\(v^2=7^2×(3^2+4^2)\)
\(v^2=7^2×(9+16)\)
\(v^2=7^2×25\)
\(v=7×5\)
\(v=35[m/s]\)
となりました。
