
斜方投射の問題では、物体の軌道は放物線を描きます。これを二次関数ととらえて問題を解こうとすると、とても複雑な式変形が必要になります。
そこで、数学とは違ったアプローチで解法を導いていきましょう。
物理では鉛直方向に適用される物理法則と、水平方向に適用される物理法則とが、それぞれ独立して運動を支配しています。
なので、高さに関する情報を知りたいときには鉛直方向のことだけ考えればよく、また、横方向に関する情報を知りたいときにも水平方向のことだけ考えれば、解を得ることができます。
なので、まずやるべきことは初速度を縦と横に分解して、斜め方向に投げられた物体が、実質、縦向きにはどのくらいで投げられたことになるのか、横方向にはどのくらいの速度で投げられたことになるのかを、それぞれ求めるところから全てはスタートします。
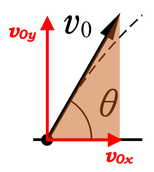
(1)
まず、初速度を縦と横に分解しましょう。分解の仕方は、特に難しく考える必要はなくて、矢印の先の点の座標を表すように縦横に補助線を引けばすぐに求まります。
そして、初速度の縦と横の成分をそれぞれ図のように\(v_{0y}\)、\(v_{0x}\)と置くことにして、\(v_{0x}\)を水平初速度、\(v_{0y}\)を鉛直初速度と呼ぶことにします。
これらの大きさは、三角比のもともとのルールから式変形します。
\(sin\theta=\displaystyle\frac{v_{0y}}{v_0}\)
\(cos\theta=\displaystyle\frac{v_{0x}}{v_0}\)
なので、それぞれ両辺を\(v_0\)倍すると、
\(v_0sin\theta=v_{0y}\)
\(v_0cos\theta=v_{0x}\)
となります。この問題の場合であれば、さらに単位も書かなければいけませんので、
\(v_{0x}=v_0cos\theta\) [m/s]
\(v_{0y}=v_0sin\theta\) [m/s]
(2)
最高点に到達するとき、縦軸方向の速さは\(0\)になるので、縦軸方向には単なる鉛直投げ上げ運動をしているととらえて、
\(v=v_0-gt\) より
\(0=v_{0y}-gt\)
\(gt=v_{0y}\)
\(t=\displaystyle\frac{v_{0y}}{g}\)
\(t=\displaystyle\frac{v_0sin\theta}{g}\) [s]
高さに関しても、初速度だけ気を付けて、単なる鉛直投げ上げ運動であるととらえて、
\(y=v_0t-\displaystyle\frac{1}{2}gt^2\) より
\(h=v_{0y}・t-\displaystyle\frac{1}{2}gt^2\)
\(h=v_0sin\theta・\displaystyle\frac{v_0sin\theta}{g}-\frac{1}{2}g(\frac{v_0sin\theta}{g})^2\)
\(h=\displaystyle\frac{v_0^2sin^2\theta}{g}-\displaystyle\frac{g}{2}・\frac{v_0^2sin^2\theta}{g^2}\)
\(h=\displaystyle\frac{v_0^2sin^2\theta}{g}-\displaystyle\frac{v_0^2sin^2\theta}{2g}\)
\(h=\displaystyle\frac{2v_0^2sin^2\theta}{2g}-\displaystyle\frac{v_0^2sin^2\theta}{2g}\)
\(h=\displaystyle\frac{v_0^2sin^2\theta}{2g}\) [m]
(3)
小球が落下するまでにかかる時間を\(t_2\)とすると、運動の対称性より、
\(t_2=2t\)
\(t_2=\displaystyle\frac{2v_0sin\theta}{g}\)
この時間だけかけて、横方向には等速直線運動をしているとみなして、
\(l=v_{0x}・t_2\) より
\(l=v_0cos\theta・\displaystyle\frac{2v_0sin\theta}{g}\)
\(l=\displaystyle\frac{2v_0^2sin\theta cos\theta}{g}\)
\(l=\displaystyle\frac{v_0^2sin2\theta}{g}\) [m]
(4)
これは答えだけ知っておいて、\(45°\)をポンと書いてもよさそうな気はしますが、一応きちんと導出しておきましょうか。
最大到達距離は
\(l=\displaystyle\frac{v_0^2sin2\theta}{g}\)
のうち、\(v_0\)と\(g\)は投げる角度を変えても同じ値なので、結局\(sin2\theta\)が最大となればいいわけですね。
\(sin\)関数はどんな値をとったとしても、必ず\(-1\)~\(1\)の間でしか変化をしないので、最大値となるということは、
\(sin2\theta=1\) となればいいわけです。
\(2\theta\)の部分をまとめて一つの角度だと考えれば、\(2\theta=90°\)であれば、この式は成立するので、結局、
\(\theta=45°\)
が、最大到達距離になるために取らなければいけない角度です。
