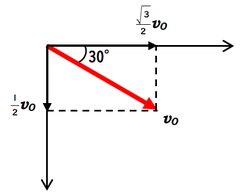
初速度が斜め向きになっているので、縦横に分解してみましょう。
伏角\(30°(-30°)\)なので、\(\sin30°\)や\(\cos30°\)を使わなくても、\(1:2:\sqrt{3}\)の関係で値を導くことができます。
問題を解く前に先に図のように\(\displaystyle\frac{1}{2}v_0\)や、\(\displaystyle\frac{\sqrt{3}}{2}v_0\)を求めておくと、後々が楽になります。
他にも、問題に\(v_0=\sqrt{gh}\)の設定がなされていますが、これは先に入れると文字数が増えて大変そうなので、最後に代入することにします。
(1)
初速度\(\displaystyle\frac{1}{2}v_0\)の鉛直投げ下ろしの問題として考えます。
鉛直下向きを正として、
\(y=v_0t+\displaystyle\frac{1}{2}gt^2\) より
\(h=\displaystyle\frac{1}{2}v_0t+\frac{1}{2}gt^2\)
\(2h=v_0t+gt^2\)
\(gt^2+v_0t-2h=0\)
解の公式より、\(t>0\)なので正の解だけ考えて、
\(t=\displaystyle\frac{-v_0+\sqrt{v_0^2-4・g・(-2h)}}{2g}\)
\(t=\displaystyle\frac{-v_0+\sqrt{v_0^2+8gh}}{2g}\)
\(v_0=\sqrt{gh}\) を代入して、
\(t=\displaystyle\frac{-\sqrt{gh}+\sqrt{gh+8gh}}{2g}\)
\(t=\displaystyle\frac{-\sqrt{gh}+\sqrt{9gh}}{2g}\)
\(t=\displaystyle\frac{-\sqrt{gh}+3\sqrt{gh}}{2g}\)
\(t=\displaystyle\frac{2\sqrt{gh}}{2g}\)
\(t=\displaystyle\sqrt{\frac{h}{g}}\)
(2)
x軸方向には、等速直線運動を行うので、
\(x=v_0t\) より
\(l=\displaystyle\frac{\sqrt{3}}{2}v_0t\)
(1)より \(t=\displaystyle\sqrt{\frac{h}{g}}\) なので
\(l=\displaystyle\frac{\sqrt{3}}{2}v_0・\sqrt{\frac{h}{g}}\)
\(v_0=\sqrt{gh}\) も代入して、
\(l=\displaystyle\frac{\sqrt{3}}{2}・\sqrt{gh}・\sqrt{\frac{h}{g}}\)
\(l=\displaystyle\frac{\sqrt{3}}{2}・\sqrt{\frac{gh・h}{g}}\)
\(l=\displaystyle\frac{\sqrt{3}}{2}h\)
(3)
着氷する瞬間の小球の速度の\(x、y\)成分をそれぞれ\(v_x、v_y\)とすると、
\(x\)成分は等速直線運動によって初めの値と同じなので、
\(v_x=\displaystyle\frac{\sqrt{3}}{2}v_0\)
\(y\)成分は鉛直投げ下ろしと考えて、
\(v_y=v_0+gt\) より
\(v_y=\displaystyle\frac{1}{2}v_0+gt\)
落下時間は(1)より
\(t=\displaystyle\sqrt{\frac{h}{g}}\) なので
\(v_y=\displaystyle\frac{1}{2}v_0+g\sqrt{\frac{h}{g}}\)
\(v_y=\displaystyle\frac{1}{2}v_0+\sqrt{gh}\)
\(v_0=\sqrt{gh}\) なので
\(v_y=\displaystyle\frac{1}{2}v_0+v_0\)
\(v_y=\displaystyle\frac{3}{2}v_0\)
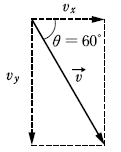
ここまで来たら、一般的には、図のように三平方の定理を用いて、斜辺に相当する部分の速さを求めます。
\(v^2=v_x^2+v_y^2\) より
\(v^2=(\displaystyle\frac{\sqrt{3}}{2})^2v_0^2+(\frac{3}{2})^2v_0^2\)
\(v^2=\displaystyle\frac{3}{4}v_0^2+\frac{9}{4}v_0^2\)
\(v^2=3v_0^2\)
\(v=\sqrt{3}v_0\)
\(v=\sqrt{3gh}\)
ただし、この問題に限り、\(v_x\)と\(v_y\)が求まった時点で、その比が\(1:\sqrt{3}\)だということに気づけば、
\(1:2:\sqrt{3}\)の関係から、\(v=2v_x\)として、一発で
\(v=\sqrt{3gh}\)
としてもいいですね。
