電流計と電圧計の内部構造

電流計と電圧計の基本構造は同じで、どちらも計器を流れる電流に比例して指針が振れるしくみになっています。
図のようにコイルに電流が流れると、フレミングの法則が適用されるような向きに可動コイルが磁石から力を受けます。
コイルが回転していく力のブレーキ役になるのがひげゼンマイで、コイルが回転していくと、ひげゼンマイがばねのように復元力を持つようになります。
このひげぜんまいの復元力とコイルが回転しようとする力がつりあう角度まで指針が振れて、ある角度で止まります。どのくらいの電流を流すとどのくらいの角度で止まるかを調べて、その角度ごとに目盛りを振っておくと、計器が完成するわけです。
このとき、電流がいくらになるかで目盛り盤を作れば「電流計」になりますし、電圧がいくらになるかで目盛り盤を作れば「電圧計」になるわけです。なので、仕組みとしては完全に同じで、違う部分というのは目盛り盤の目盛りの振り方だけということになります。
分流器

\(I_0[A]\)までの電流をはかることができる内部抵抗\(rA[\Omega]\)の電流計があったとします。この電流計に\(I_0[A]\)以上流すと、先ほどの仕組みに従えば、針が回転しすぎて目盛り盤を振り切ってしまうことになります。
では、大きい電流を測定したいときにはどうすればいいでしょうか。
これを用いて\(nI_0[A]\)までの電流をはかるようにするには、分岐路を作って、電流計の測定する部分に大きい電流が流れないようにすればいいわけです。このとき、構造としては、電流計と並列に抵抗を接続して分岐路をつくればいいですね。
電流計の測定部分には\(I_0[A]\)が流れ、残りの\(nI_0-I_0[A]\)は、分岐したほうの回路に流れることになります。このとき、分岐路の方に設置した抵抗を、電流計の分流器といいます。
分流器の抵抗値を\(R_A[\Omega]\)とすると、並列部分の電圧は等しいことから、
\(r_AI_0=R_A(n-1)I_0\)
\(r_A=R_A(n-1)\)
\(R_A=\displaystyle\frac{r_A}{n-1}\)
となり、この大きさの抵抗を分流器として接続してやると、限界値より大きい電流を測定できるような電流計を作成することができます。
▼分流器の抵抗値
\(R_A=\displaystyle\frac{r_A}{n-1}\)
文字式だとイメージしにくいので、数字を入れてちょっと考えてみましょうか。
問:内部抵抗が\(5.0×10^{-2}[\Omega]\)、測定範囲\(10mA\)の電流計がある。この電流計で\(1[A]\)まで測定できるようにするためには何\(\Omega\)の分流器を並列接続すればよいか。
解説:
分流器公式を使えば、電流を\(100\)倍まで流せるようにしたいので、\(n=100\)として、
\(R_A=\displaystyle\frac{r_A}{n-1}\) より
\(R_A=\displaystyle\frac{5.0×10^{-2}}{100-1}\)
\(≒5.1×10^{-4}[\Omega]\)
でいいんですが、考え方を知っている方が公式を忘れたときや変則的な問題が出たときに対応できますので、改めて考え方を重視して解いてみます。
\(10mA\)しか測定できないところに\(1A\)、つまり\(1000mA\)を流そうとしているわけです。すると電流計は壊れますから、余分な\(990mA\)を分流器に逃がします。
オームの法則を電流計と分流器のそれぞれに適用すると、
\(V=r_A×10[mA]\)
\(V=R_A×990[mA]\)
となりますが、並列部分は電圧が等しいので、
\(990R_A=10r_A\)
あとはここに\(r_A=5.0×10^{-2}[\Omega]\)を代入して整理したら解答完成と、そういうことです。
倍率器
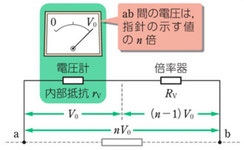
同様に、今度は電圧計について考えてみましょう。
\(V_0[V]\)までの電圧をはかることができる内部抵抗\(rV[\Omega]\)の電圧計があったとします。これを用いて\(nV_0[V]\)までの電圧をはかるようにするには、電圧計と直列に抵抗を接続すればいいことになります。このときに接続する抵抗を、電圧計の倍率器といいます。
電圧計は測定したい抵抗に並列に接続して使います。なので、測定したい抵抗にかかる電圧が大きいときは、回路の性質によって並列部分の電圧が等しいため、電圧計にも大きい電圧がかかってしまうことになります。すると針が降り切れて測定できなくなります。
電流計の場合は、余分に流れる電流を別コースに逃がしてやることで解決させましたが、電圧計の場合は余分な電流を逃がすと測定したい抵抗にかかる電圧が変わってしまうため、そういう操作ができない制約があります。
そこで考え方を変えます。並列部分は電圧が等しく、そして何より測定したい抵抗に並列に接続していますので、電圧計の先にでっかい抵抗をつけて、そもそも電圧計に電流が流れこまないようにしてしまうのがいいでしょう。
電圧計に流れる電流が小さくても、並列部分の電圧は等しいので、全然問題はないわけです。むしろ、本来測定したい抵抗に流れていたはずの電流を奪ってきて測定するので、電圧計を接続することで回路の値には狂いが生じてしまいます。電圧計がもつ抵抗が大きいと、回路から奪ってくる電流が少なくて済みますので、むしろ好都合です。
そして図のようになります。抵抗にかかる電圧を\(nV_0[V]\)にしたとき、電圧計と倍率器あわせて\(nV_0[V]\)になるように調整をしてやると、倍率器にかかる電圧が\((n-1)V_0[V]\)になります。
電圧計と倍率器のそれぞれについてオームの法則を適用すると、
\(V_0=r_VI\)
\((n-1)V_0=R_VI\)
であるから、流れる電流は、
\(I=\displaystyle\frac{V_0}{r_V}\)
\(I=\displaystyle\frac{(n-1)V_0}{R_V}\)
電圧計と倍率器は直列に接続されていて電流は等しいので、
\(\displaystyle\frac{V_0}{r_V}=\frac{(n-1)V_0}{R_V}\)
よって
\(R_V=(n-1)r_V\)
これが倍率器の抵抗値ということになります。
▼倍率器の抵抗
\(R_V=(n-1)r_V [\Omega]\)
