インピーダンス

交流回路における合成抵抗のことを「インピーダンス」といいます。交流電源に接続した回路素子も、抵抗だけの回路のように合成抵抗を考えることができるはずです。
ところがこれらの回路素子は交流につなぐと電流や電圧がそれぞれズレてしまうため、統一的に考えるには工夫しなければいけません。
方針としては、直列につないで合成するときには、電流がどこでも同じである必要性があって、並列につないで合成するときは、電圧がどこでも同じになっている必要があります。
その指針のもとで導出すると、最終的に以下のようなインピーダンスが導けます。
▼RLC回路のインピーダンス
[直列合成]
\(Z=\sqrt{R^2+\left( \omega L - \displaystyle\frac{1}{\omega C}\right)^2}\)
[並列合成]
\(Z=\displaystyle\frac{1}{\sqrt{(\frac{1}{R})^2+( \omega C - \frac{1}{\omega L})^2}}\)
RLC直列合成
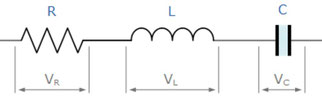
抵抗とコイル、コンデンサーを直列につないだときのインピーダンスを計算してみましょう。ここに交流電源をつないだとします。すると、電流の正負は頻繁に入れ替わりますが、どの瞬間を考えたとしても、直列接続ですので、どの素子に流れる電流も値は変わりません。
そこで、電源から\(I=I_0\sin\omega t\)の電流が流れ、3つの回路素子それぞれに\(I=I_0\sin\omega t\)が等しく流れていると考えましょう。
▼\(Step1\) まず、それぞれの素子にかかる電圧を導出します。
■抵抗\(R\)について
\(V_R=RI\) より
\(V_R=RI_0\sin\omega t\)
■コイル\(L\)について
\(V_L=L\displaystyle\frac{dI}{dt}\) より
\(V_L=L\displaystyle\frac{d}{dt}I_0\sin\omega t\)
\(V_L=\omega LI_0\cos\omega t\)
■コンデンサー\(C\)について
\(I=\displaystyle\frac{dQ}{dt}\) に、\(Q=CV_C\)を代入して、(ついでに\(I=I_0\sin\omega t\)として)
\(I_0\sin\omega t=\displaystyle\frac{d}{dt}CV_C\)
両辺\(t\)で積分すると、
\(I_0\displaystyle\int \sin\omega t dt=CV_C\)
\(-\displaystyle\frac{I_0}{\omega} \cos\omega t =CV_C\)
\(V_C=-\displaystyle\frac{I_0}{\omega C} \cos\omega t \)
▼\(Step2\) つぎに、これらの電圧の合計を計算します。
\(V= V_R + V_L + V_C\) より
\(V= RI_0\sin\omega t + \omega LI_0\cos\omega t -\displaystyle\frac{I_0}{\omega C} \cos\omega t \)
\(V= RI_0\sin\omega t+\left(\omega L-\displaystyle\frac{1}{\omega C}\right) I_0 \cos\omega t \)
ここで、三角関数の合成公式
\(a\sin\theta + b\cos\theta=\sqrt{a^2+b^2}\sin(\theta + \alpha)\)
を使うと、
\(V=\sqrt{\left(RI_0\right)^2+\left(\omega L-\displaystyle\frac{1}{\omega C}\right)^2I_0^2} \sin(\omega t +\alpha)\)
よって、
\(V=\sqrt{R^2+\left(\omega L-\displaystyle\frac{1}{\omega C}\right)^2} I_0 \sin(\omega t +\alpha)\)
このとき、この式を大きく\(V=RI\)の塊としてみてやると、ルートの部分が抵抗に相当しますので、これをまとめてRLC直列回路のインピーダンスとして扱います。ただし、いわゆる回路中にある普通の抵抗とは種類の違う”抵抗のような働きのもの”ですので、\(R\)ではなく\(Z\)で特徴づけてやります。
▼RLC直列回路のインピーダンス
[直列合成]
\(Z=\sqrt{R^2+\left( \omega L - \displaystyle\frac{1}{\omega C}\right)^2}\)
RLC並列合成
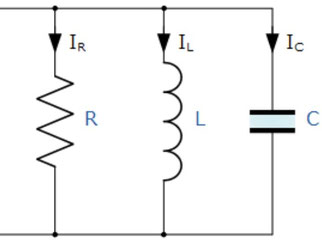
次に、抵抗とコイル、コンデンサーを並列につないだ場合を考えてみます。
今度は、並列接続ですので、電流の大きさは素子ごとに違っても構いません。その代わり、電圧はどの素子にも等しくかかりますので、3つの回路素子それぞれに\(V=V_0\sin\omega t\)の電圧が等しくかかっているいると考えましょう。
▼\(Step1\) まず、それぞれの素子にかかる電流を導出します。
これは前回の「電磁気29」で途中段階を追っていますので、結果を持ってくることにしましょう。(※電磁気29は未編集)
■抵抗\(R\)について
\(I_R=\displaystyle\frac{V_0}{R}\sin\omega t\)
■コイル\(L\)について
\(I_L=-\displaystyle\frac{V_0}{\omega L}\cos\omega t\)
■コンデンサー\(C\)について
\(I_C=\omega CV_0\cos\omega t\)
▼\(Step2\) つぎに、これらの電流の合計を計算します。
\(I= I_R + I_C + I_L\) より
\(I= \displaystyle\frac{V_0}{R}\sin\omega t + \omega CV_0\cos\omega t - \frac{V_0}{\omega L}\cos\omega t\)
\(I= \displaystyle\frac{V_0}{R}\sin\omega t +\left( \omega C-\frac{1}{\omega L}\right)V_0\cos\omega t\)
ここで、三角関数の合成公式
\(a\sin\theta + b\cos\theta=\sqrt{a^2+b^2}\sin(\theta + \alpha)\)
を使うと、
\(I=\sqrt{\left( \displaystyle\frac{V_0}{R}\right)^2+\left(\omega C-\displaystyle\frac{1}{\omega L}\right)^2V_0^2} \sin(\omega t +\alpha)\)
よって、
\(I=\sqrt{\left( \displaystyle\frac{1}{R}\right)^2+\left(\omega C-\displaystyle\frac{1}{\omega L}\right)^2} V_0\sin(\omega t +\alpha)\)
このとき、この式を大きく\(I=\frac{V}{R}\)の塊としてみてやると、ルートの部分が\(\frac{1}{R}\)に相当しますので、このルートの部分の逆数をとって、
\(Z=\displaystyle\frac{1}{\sqrt{\left( \displaystyle\frac{1}{R}\right)^2+\left(\omega C-\displaystyle\frac{1}{\omega L}\right)^2}}\)
とし、これをまとめてRLC並列回路のインピーダンスとして扱います。
▼RLC並列回路のインピーダンス
[並列合成]
\(Z=\displaystyle\frac{1}{\sqrt{(\frac{1}{R})^2+( \omega C - \frac{1}{\omega L})^2}}\)
