ドップラー効果

救急車がサイレンを鳴らしながら走っているとき、その救急車が近づくときに音は高く聞こえ、遠ざかるときには音が低くなります。
このような現象を「ドップラー効果」といいます。
ドップラー効果は、音波だけに関わらず、水面波や光波、電波などでも起こりますので、波動全般でみられる現象です。
図のように、\(x\)軸正の向きに等速で運動している波源から波を発生させると、その周囲に特徴的な波面ができます。発生する波の山の部分を図の実線で示したとすると、波源の運動する方向の前方では波の間隔が短くなり、波源の運動する方向の後方では波の間隔が長くなります。
その結果、運動する波源の前方に観測者がいれば、振動数の大きい音、つまり高い音を観測し、運動する波源の後方に観測者がいれば、振動数が小さい音、つまり低い音を観測する、という仕組みになっているわけです。
しかもですね、1波長を音1個とカウントして、例えば図のように音源から10個の音が出ているとします。10個の音が出た後、音源は音を鳴らすのをやめてしまうことにしましょうか。
一度音源から音が出てしまえば、あとは音速は一緒ですので、それも含めて考えると、高い音が聞こえる時間は短くて、低い音が聞こえる時間は長いことになります。1つ目の音を聞いてから、10個目の音を聞くまでの時間が違うということです。
また、波の回折の特徴を考えると、音源の前方では波長が短いので、あまり回折することがない一方で音源の後方では波長が長いので回折は前方と比較すると大きくなる、という特徴もあります。
私の経験ですと、街中で救急車がどこかから近づくとき、近づきつつあるときには回折が小さいため、音に気付きにくい一方、通り過ぎてしまうと回折が大きくなるので、救急車が通り過ぎたな、ということがわかります。
そんな経験はありませんか?私だけですか?この一文はそれぞれの学校の先生方がどう解釈するのか気になるところですね。錯覚かもしれません。
音源が動く場合のドップラー効果
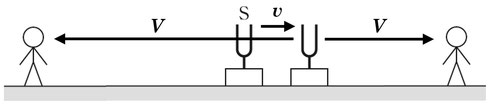
図のように振動数\(f_0\)の音を出す音源が右向きに速さ\(v\)で動いていて、その前後に静止している観測者がいるとします。風は吹いておらず音速は\(V\)であるとしておきましょう。
■観測者が音源の後方(図の左)にいるとき
音源から見た音についての波の基本式(\(V=f\lambda\))を考えます。音速は\(V\)ですが、音源が音の進む方向と反対側に\(v\)で進むので、音源から見れば音速は\(V+v\)になっています。振動数は自分自身が音源ですので音源から音源を観測すれば当然\(f_0\)のままでしょう。また、波長は一つ前の図の通り、音源の後方では長くなっているはずですので、とりあえず\(\lambda_左\)としておきます。
すると音源から見たときの波の基本式は
\(V+v=f_0\lambda_左\)
となります。
また、その後、観測者がとらえる音についての波の基本式も考えてみようと思います。音は空気中に放出されてしまった後は、ただの空気の振動ですので、音源の運動状況によらず音速\(V\)で伝わります。ところがドップラー効果が起こりますので、観測者がとらえる音は、音源から出る振動数\(f_0\)とは違う値になるはずです。これを\(f\)とすることにします。また、波長は音源側から見ようと観測者側から見ようと同じですので、\(\lambda_左\)はそのまま同じです。
よって、観測者から見たときの波の基本式は
\(V=f\lambda_左\)
となります。これら二つの式を連立すると、
\(\displaystyle\frac{V+v}{V}=\frac{f_0\lambda_左}{f\lambda_左}\)
\(\displaystyle\frac{V+v}{V}=\frac{f_0}{f}\)
\(f=\displaystyle\frac{V}{V+v}f_0\)
となります。これが、音源が遠ざかるときのドップラー効果の振動数の式です。
■観測者が音源の前方(図の右)にいるとき
同様に考えると、\(+v\)のところを\(-v\)にすればいいだけですので、音源から見た音の波の基本式は、
\(V-v=f_0\lambda_右\)
となり、観測者がとらえる音の波の基本式は、
\(V=f\lambda_右\)
となりますので、音源が近づくときのドップラー効果の振動数の式は、
\(f=\displaystyle\frac{V}{V-v}f_0\)
となります。
観測者が動く場合のドップラー効果

今度は、音源が静止していて、観測者が等速度\(v\)で近づいたり遠ざかったりしている場合を考えてみましょう。
■観測者が音源に近づく場合
これも考え方自体は同じです。音源から見た音についての波の基本式と、観測者から見た音の波の基本式を連立します。
音源から見た音の波の基本式は、何も加工するところがありませんので、
\(V=f_0\lambda\)
です。
一方で、観測者から見た音は、自ら音に向かって突き進んでいますので、音速を\(V+v\)としてとらえることになります。そしてその結果、ドップラー効果が起こりますので、音源から出ているものと異なる振動数\(f\)を受けることになります。波長\(\lambda\)については観測者が動こうが止まろうが関係なく\(\lambda\)ですね。
よって、観測者から見た音の波の基本式は、
\(V+v=f\lambda\)
となります。これら2つを連立すると、
\(\displaystyle\frac{V}{V+v}=\frac{f_0\lambda}{f\lambda}\)
\(\displaystyle\frac{V}{V+v}=\frac{f_0}{f}\)
\(f=\displaystyle\frac{V+v}{V}f_0\)
となり、これが観測者が近づくときのドップラー効果の振動数の式となります。
■観測者が音源から遠ざかる場合
同様に、\(+v\)のところを\(-v\)として考えましょう。
音源から見た音の波の基本式は、何も加工するところがありませんので、
\(V=f_0\lambda\)
で、観測者から見た音の波の基本式は、
\(V-v=f\lambda\)
となります。これら2つを連立すると、
\(\displaystyle\frac{V}{V-v}=\frac{f_0\lambda}{f\lambda}\)
\(f=\displaystyle\frac{V-v}{V}f_0\)
となり、これが観測者が遠ざかるときのドップラー効果の振動数の式となります。
実際はこれら4パターンを場合分けせずに、すべて統合して一つの式にまとめてしまうのがいいでしょう。
▼ドップラー効果
\(f=\displaystyle\frac{V-v_o}{V-v_s}f_0\)
\(f[Hz]\):見かけの振動数 \(f_0[Hz]\):音源の振動数
\(V[m/s]\):音速
\(v_o[m/s]\):観測者が音源から離れる速さ
\(v_s[m/s]\):音源が音の向きに進む速さ
