偶力

同じ大きさで、逆向きに働いているけれど、同一直線上にはない力のことを「偶力」といいます。
偶力は図のように2つの力で1対のものとして考えます。
偶力の合力はゼロということになります。また、合力がゼロですが、力のモーメントはゼロでない、という特性を持つことになります。
なので、力のはたらきとしては、物体を平行移動させることはないが、回転運動させることはできる、ということになります。
これが偶力と、その特性です。
偶力の計算例
では、偶力がつくる力のモーメントがいくらになるのか、ということを考えてみましょう。
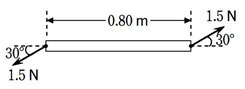
図のように、長さ\(0.80m\)で一様な棒の両端に偶力がかかっています。
これらがつくる力のモーメントを考えるとき、棒の中心は動きませんので、仮にここを原点と考えましょう。
力のモーメントは「力の大きさ×棒の長さ」で計算できますが、力の大きさは棒に対して垂直な成分だけを考えます。
いま、力の棒に垂直な成分は\(0.75[N]\)ですね。
左の力が作る力のモーメントは、
\(M=FL\) より
\(M_左=0.75×0.40\)
\(M_左=0.30[N・m]\)
右の力が作る力のモーメントも、
\(M_右=0.75×0.40\)
\(M_右=0.30[N・m]\)
となりますので、その和は
\(M=M_左+M_右\)
\(M=0.30+0.30\)
\(M=0.60[N・m]\)
と求まります。
ですが、偶力を計算すると、左右どちらもいつでも同じ値になります。
なので2力を1対としてまとめて考えて、
\(0.75[N]\)の偶力が、長さ\(0.80[m]\)の棒に加わっている、と解釈して、
\(M=0.75×0.80\)
\(M=0.60[N・m]\)
としてしまった方が圧倒的に計算が速くなります。
これを偶力のモーメントの式、とすることにします。
▼偶力のモーメント
\(M=FL\) \([N・m]\)
\(F[N]\):偶力 \(L[m]\):棒の長さ(偶力間の直線距離)
