(ア) ヤング
(イ)(ウ)
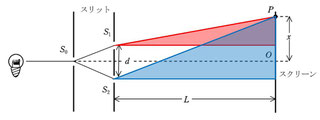
まず、図のように、\(S_1\)と\(S_2\)からスクリーンに垂線を引いて、直角三角形を二つ作ります。
この直角三角形のそれぞれで、三平方の定理を適用しましょう。
\(\overline{S_1P}^2=l^2+\left(x-\displaystyle\frac{d}{2}\right)^2\)
\(S_1P=\sqrt{l^2+\left(x-\displaystyle\frac{d}{2}\right)^2}\)
\(\overline{S_2P}^2=l^2+\left(x+\displaystyle\frac{d}{2}\right)^2\)
\(S_2P=\sqrt{l^2+\left(x+\displaystyle\frac{d}{2}\right)^2}\)
(エ)
これらを引き算すると、
\(S_2P-S_1P= \sqrt{l^2+\left(x+\displaystyle\frac{d}{2}\right)^2}-\sqrt{l^2+\left(x-\displaystyle\frac{d}{2}\right)^2}\)
ここで、近似を使うために、\(l\)をくくります。
\(S_2P-S_1P= l\sqrt{1+\displaystyle\frac{\left(x+\frac{d}{2}\right)^2}{l^2}}-l\sqrt{1+\displaystyle\frac{\left(x-\frac{d}{2}\right)^2}{l^2}}\)
\(S_2P-S_1P= l\left[1+\displaystyle\frac{\left(x+\frac{d}{2}\right)^2}{l^2}\right]^{\frac{1}{2}}-l\left[1+\displaystyle\frac{\left(x-\frac{d}{2}\right)^2}{l^2}\right]^{\frac{1}{2}}\)
問題文に、\(\alpha\)が十分小さいとき、\((1+\alpha)^{\frac{1}{2}}=1+\frac{1}{2}\alpha\)と近似できるとあります。
\(S_2P-S_1P= l\left[1+\displaystyle\frac{\left(x+\frac{d}{2}\right)^2}{2l^2}\right]-l\left[1+\displaystyle\frac{\left(x-\frac{d}{2}\right)^2}{2l^2}\right]\)
\(S_2P-S_1P= l+\displaystyle\frac{\left(x+\frac{d}{2}\right)^2}{2l}-l-\displaystyle\frac{\left(x-\frac{d}{2}\right)^2}{2l}\)
\(S_2P-S_1P= \displaystyle\frac{\left(x+\frac{d}{2}\right)^2}{2l}-\displaystyle\frac{\left(x-\frac{d}{2}\right)^2}{2l}\)
\(S_2P-S_1P= \displaystyle\frac{1}{2l}\left(x+\frac{d}{2}\right)^2-\displaystyle\frac{1}{2l}\left(x-\frac{d}{2}\right)^2\)
\(S_2P-S_1P= \displaystyle\frac{1}{2l}\left(x^2+xd+\frac{d^2}{4}\right)-\frac{1}{2l}\left(x^2-xd+\frac{d^2}{4}\right)\)
\(S_2P-S_1P= \displaystyle\frac{x^2}{2l}+\frac{xd}{2l}+\frac{d^2}{8l}-\frac{x^2}{2l}+\frac{xd}{2l}-\frac{d^2}{8l}\)
\(S_2P-S_1P= \displaystyle\frac{xd}{l}\)
(オ)
経路差が波長の整数倍のときに光が強め合うので、
\(m\lambda\)
(カ)
\(\displaystyle\frac{xd}{l}=m\lambda\) より、
\(m=0\)のとき、\(x_0=0\)
\(m=1\)のとき、\(\displaystyle\frac{x_1d}{l}=\lambda\)
つまり、\(x_1=\displaystyle\frac{l\lambda}{d}\)
であるから、明線間隔は、
\(\Delta x=x_1-x_0=\displaystyle\frac{l\lambda}{d}\)
ここに各値を代入すると、
\(\Delta x=\displaystyle\frac{4.5×10^{-7}}{0.10×10^{-3}}\)
\(\Delta x=4.5×10^{-3}[m]\)
(キ)
(カ)と同様に、\(\lambda=6.0×10^{-7}[m]\)の光についても明線間隔を求めると、
\(\Delta x=\displaystyle\frac{l\lambda}{d}\) より
\(\Delta x=\displaystyle\frac{6.0×10^{-7}}{0.10×10^{-3}}\)
\(\Delta x=6.0×10^{-3}[m]\)
となります。あとは、これら二つの光の明線間隔の最小公倍数を探してやるといいでしょう。
青色光の明線が現れるのが、
\(0[m]\)
\(0.45×10^{-2}[m]\)
\(0.90×10^{-2}[m]\)
\(1.35×10^{-2}[m]\)
\(1.80×10^{-2}[m]\)
\(2.25×10^{-2}[m]\)
と続き、赤色光の明線が現れるのが、
\(0[m]\)
\(0.60×10^{-2}[m]\)
\(1.20×10^{-2}[m]\)
\(1.80×10^{-2}[m]\)
\(2.40×10^{-2}[m]\)
と続くので、明線が重なるのが、
\(0[m]\)
\(1.80×10^{-2}[m]\)
のときなので、間隔は有効数字を2桁に丸めて、
\(1.8×10^{-2}[m]\)
となります。
