ビオ・サバールの法則
電流が作る磁束密度の場は、ビオ・サバールの法則か、もしくはアンペールの法則によって表すことができます。
これは、高校範囲でいうところの、右ねじの法則に相当するようなものです。
電流を流すと、その周囲に磁場が発生しますが、このときに流す電流が時間的に変化すると、右ねじの法則とは別の説明が追加されてしまいますので、今は流す電流が一定の状態(定常電流という)を考えることにします。
歴史的な流れや先人の苦労した厳密な部分を置いといて、おいしいところだけもらいながら説明していきます。
1820年、デンマークの物理学者エールステッドが、コペンハーゲン大学で講義中に、電流を流した導線近くに置いた方位磁針が動くことを発見しました。右ねじの法則の現象の発見です。
これに対して、フランスの物理学者ビオとサバールは共同で研究を進め、微小長さの導線に電流が流れると、そこからある距離離れたところに磁場が発生しているということを立式化しました。
クーロンの法則から、電場が
\(E=k\displaystyle\frac{Q}{r^2}=\frac{1}{4\pi \varepsilon_0}\frac{Q}{r^2}\)
と書けるのと同じように、磁束密度は
\(B=k'\displaystyle\frac{I}{r^2}=\frac{\mu_0}{4\pi}\frac{I}{r^2}\)
と書けると類推したわけです。ただし、電流要素の部分は、点電荷のように扱わなければならない都合上、
\(B=\displaystyle\frac{\mu_0}{4\pi}\frac{I\Delta s}{r^2}\)
と表記すれば物理的なことを考慮した上で対応させることができます。
これがビオ・サバールの法則の骨組みの部分です。
ところが、扱っている電流が小さな破片で存在することはありません。電流の微小要素という概念はあくまで理論上の産物であって、導線の全領域にわたって足し合わせなければ実験結果との整合性は合わないはずです。
なので、左辺の磁束密度は、概念でしかない微小電流によって作られる微小な磁束密度にすぎないはずですので、
\(\Delta B=\displaystyle\frac{\mu_0 I\Delta s}{4\pi r^2}\)
となります。
このとき作られる磁場の向きは、ベクトル\(\Delta \mathbf{s}\)と\(\mathbf{r}\)の両方に垂直で、右ねじを\(\Delta \mathbf{s}\)の方向から\(\mathbf{r}\)の方向に回したときにねじが進む向きになります。(そのまま周回させると、よく知られているように、直線電流を一周してできる磁場の向きになります)
この向きを数式で示そうと思うと、外積を使わざるを得なくなり、高校範囲でカバーできなくなってしまいます。
大きさが1のベクトル(単位ベクトル)を使って、大きさを変えないまま、数式に向きの情報だけ乗せるために、
\(\displaystyle\frac{\mathbf{r}}{|r|}\)
を右からかけて、
\(\Delta \mathbf{B}=\displaystyle\frac{\mu_0 I(\Delta \mathbf{s}×\mathbf{r})}{4\pi r^3}\)
となります。これがビオ・サバールの法則の式です。繰り返しになりますが、基本構造としては、電場の式の磁束密度バージョンとしての、
\(B=k'\displaystyle\frac{I}{r^2} , \Delta B=k'\displaystyle\frac{\Delta I}{r^2}\)
ですので、それを知っていると覚えやすいでしょう。
▼ビオ・サバールの法則
\(\Delta \mathbf{B}=\displaystyle\frac{\mu_0 I(\Delta \mathbf{s}×\mathbf{r})}{4\pi r^3}\)
\(\Delta \mathbf{B}\):微小電流が作る磁束密度 \(\mu_0\):真空の透磁率
\(\Delta \mathbf{s}\):電流の微小長さの要素 \(\mathbf{r}\):微小電流からの距離
アンペールの法則
同時期に、ビオやサバールとは別に、アンペールがエールステッドの実験結果を数式にまとめることに成功しました。
1820年、エールステッドの発見後すぐに「アンペールの規則(Ampère's rule)」を提唱しました。これは「スイマー(swimmer)の法則」とも言われ、電流の流れに対して磁場が周回しているという向きに関する情報を、泳いでいる人がクルクルと回転しながら前にすすむイメージに例えて呼ばれていました。
その後、1822年には数式で説明することにも成功し、「アンペールの法則(Ampère's law)」と名前が変更されました。
次のように式で表されます。
\(\displaystyle\oint_C\mathbf{B}・d\mathbf{s}=\mu_0I\)
アンペールはビオやサバールと違い、概念でしか存在しえない「微小電流」というものを初めから用いることはありませんでした。
逆に、発生する磁場が電流を軸として周回していることに着眼し、発生する磁場の接線成分を微小長さだけ求め、周回して足し合わせてやると、その値が電流と対応することを数式化しました。
微小量を足し合わせる場合の計算はサメーション(シグマ)ではなく、積分を使うのですが、このときの積分は単なる積分ではなく、経路を一周させるという特別なタイプの積分で、これを「周回積分」と呼び、積分記号にマルをつけた、\(\displaystyle \oint_C ds\)という記号を使います。添え字の\(C\)は\(Circle\)を意味していて、マルだけでなく、さらに添え字でも、周回していますよということを明確に表しています。
一般には閉曲面を周回するときに、いろんなコースを無尽蔵に設定できますので、周回しますという意味で積分にマルをつけ、その経路は\(C\)に沿って一周させていますよ、という意味合いで\(C\)も追記している、という感じでしょうか。
▼アンペールの法則
\(\displaystyle\oint_C\mathbf{B}・d\mathbf{s}=\mu_0I\)
\(\Delta \mathbf{B}\):電流が作る磁束密度 \(\mu_0\):真空の透磁率
\(\Delta \mathbf{s}\):磁束密度の微小長さの要素 \(\mathbf{r}\):電流からの距離
直線電流がつくる磁場
試しに、高校範囲で最初に習う直線電流の周囲の磁場についてアンペールの法則を使って計算してみます。
\(\displaystyle\oint_C\mathbf{B}・d\mathbf{s}=\mu_0I\) から計算しますね。
磁力線のうちの一本に着眼します。
直線電流の周囲に発生する磁場の半径は常に一定で、周回上での磁場の大きさも常に一定ですので、内積部分を考えずにそのまま積分することができます。
\(\displaystyle\oint_CBds=\mu_0I\)
\(B\)は定数ですので積分の外に出すことができて、
\(B\displaystyle\oint_Cds=\mu_0I\)
周回積分だけが残りましたが、この積分は、直線電流の周囲にできる円形磁場の、円周の長さを計算しているという意味になります。なので、
\(B×2\pi r=\mu_0I\)
よって、
\(B=\displaystyle\frac{\mu_0I}{2\pi r}\)
\(B=\mu_0H\) より
\(H=\displaystyle\frac{I}{2\pi r}\)
となり、確かに高校で習う内容と一致していますね。高校ではこの導出をせずに、いきなり公式として舞い降りてきますが、実際にはアンペールの周回積分をした計算結果がこの形だったということなんですね。
1回巻コイル中心点の磁場
次に、半径\(r\)の1回巻の円形コイルに定常電流\(I\)が流れているとします。このとき、コイルの中心の1点において、生じる磁場が \(H=\displaystyle\frac{I}{2r}\) になることを確認してみましょう。
今度はアンペールの法則ではなく、ビオ・サバールの法則から導出してみることにします。
\(dH=\displaystyle\frac{Ids}{4\pi r^2}\) から計算しますね。
これを円周にわたって積分すると、
\(\displaystyle\int dH=\oint_C\frac{Id\mathbf{s}}{4\pi r^2}\)
\(=\displaystyle\frac{I}{4\pi r^2}\oint_C d\mathbf{s}\)
\(=\displaystyle\frac{I}{4\pi r^2}・2\pi r\)
\(=\displaystyle\frac{I}{2 r}\)
となります。
この式も高校範囲では突如公式が舞い降りてきますが、本来は計算式があって、その結果にすぎないので、高校範囲では式が簡単なので「出てきた答えだけを覚えましょう」という扱いになっているということですね。
1回巻コイル中心軸上の磁場
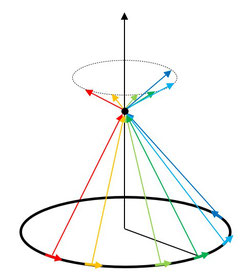
今度は、同じ円形コイルの中心の磁場を考えますけれど、中心「点」ではなく、中心「軸」での磁場の大きさを考えてみることにします。
先ほどと同様に、円形コイルの場合は、アンペールの法則ではなくビオ・サバールの法則の方が有用性が高いので、ビオ・サバールの法則で説明を進めていきます。
コイル上の微小長さに流れる電流を考えます。そして、その微小電流がコイルの中心軸のある一点につくる磁場を考えます。対称性から、軸上ではこれらの大きさが等しいため、計算は任意の一点につくる磁場を考えるよりは、まだ簡単なはずです。
微小長さが作る微小磁場を考え、それを円周にわたって積分すれば、すべてを重ね合わせたことになり、中心軸の磁場の大きさが求まるはずです。
ちなみに向きはいいですよね?図を見て明確ですが、すべて足し合わせたら水平成分が上手にすべて打ち消し合いそうですね。
数式で示してもいいでしょうが、数行で計算が終わりそうなので省略します。
こういうとき、水平成分が打ち消し合うのは「自明である」と言います。証明することができるが、書くまでもなく数行の操作で追うことができる、あるいは暗算で十分である、というときに使います。
「自明である」というのは、論証を簡単に書けるようなときに使いますので、式変形が簡単であっても、その変形を難しく感じる人にとっては「自明」ではないと思います。きちんと途中段階を書き出してみるべきと思います。

微小電流が中心から軸上に\(z\)だけ離れた点につくる微小磁場を考えます。
向きは\(l\)と垂直な向きに\(dH\)として発生します。
微小磁場の水平成分は打ち消し合いますので、使うのは軸成分\(dH\sin\theta\)だけです。
これを円周にわたって積分しましょう。
\(dH=\displaystyle\frac{Ids}{4\pi l^2}\)
\(=\displaystyle\frac{Ids}{4\pi}・\frac{1}{r^2+z^2}\)
ですので、軸成分は、
\(dH\sin\theta=\displaystyle\frac{Ids}{4\pi (r^2+z^2)}\sin\theta\)
\(dH\sin\theta=\displaystyle\frac{Ids}{4\pi (r^2+z^2)}・\frac{r}{\sqrt{r^2+z^2}}\)
\(dH\sin\theta=\displaystyle\frac{Ir}{4\pi (r^2+z^2)^{\frac{3}{2}}}ds\)
これを円周にわたって積分すると、前の議論と同じく\(2\pi r\)をかけることと同じですので、
\(H_z=\displaystyle\oint_C \frac{Ir}{4\pi (r^2+z^2)^{\frac{3}{2}}}ds=\frac{Ir}{4\pi (r^2+z^2)^{\frac{3}{2}}}\oint_C ds\)
\(H_z=\displaystyle\frac{Ir}{4\pi (r^2+z^2)^{\frac{3}{2}}}・2\pi r\)
\(H_z=\displaystyle\frac{Ir^2}{2 (r^2+z^2)^{\frac{3}{2}}}\)
となります。
\(z=0\)の場合だと、高校の公式と整合性がとれますね。
無限に長いソレノイドコイルの中心軸上の磁場
1回巻の円形コイルの中心軸の磁場が
\(H_z=\displaystyle\frac{Ir^2}{2 (r^2+z^2)^{\frac{3}{2}}}\)
となりました。これが同じ円周上に\(N\)回巻なら単純に\(N\)倍して終わりなんですが、コイルは巻くと当然厚みが出ますから、\(z\)の値はきっと変わってくるんでしょうね。
なので、巻き数を増やしたときも単純なかけ算ではなく、積分計算をすることになりそうです。
\(1[m]\)あたりの巻き数が\(n\)回のソレノイドコイルを考えます。
すると、
\(1[m]\) あたり \(n\)回
\(z[m]\) あたり \(zn\)回
\(\Delta z [m]\) あたり \(n \Delta z\)回
\(dz[m]\) あたり \(n dz\)回
の巻き数があるということですので、
\(dH_z=H_z×ndz\)
\(=\displaystyle\frac{Ir^2}{2 (r^2+z^2)^{\frac{3}{2}}}×ndz\)
これを\(-\infty\)から\(\infty\)まで、\(dz\)について積分すればいいことになります。
\(H=\displaystyle\int dH_z\)
\(=\displaystyle\int^{\infty}_{\infty}\frac{Ir^2}{2 (r^2+z^2)^{\frac{3}{2}}}×ndz\)
\(=nIr^2\displaystyle\int^{\infty}_0\frac{1}{(r^2+z^2)^{\frac{3}{2}}}dz\)
無限に長いソレノイドコイルには対称性があるので、積分区間を半分にしておいて、値を2倍しました。
で、この積分を実行したら無事\(H=nI\)にたどり着くんですが、力押ししようと思うと非常に煩雑で、なかなか式変形できないんですね。どうしたもんかと。
■積分区間の置換
そこで、\(z\)についての積分を捨てて、\(\theta\)についての積分に置換しようかと思います。そうなると、
\(z\)について:\(0\rightarrow \infty\) \(\theta\)について:\(\displaystyle\frac{\pi}{2}\rightarrow 0\)
という区間変更ですね。

■分母の分数指数の処理
\(H=nIr^2\displaystyle\int^{\infty}_0\frac{1}{(r^2+z^2)^{\frac{3}{2}}}dz\) つまり、\(H=nIr^2\displaystyle\int^{\infty}_0\frac{1}{l^3}dz\) において、
\(l\cos\theta=z\) ; \(l^3\cos^3\theta\) なので、
\(H=nIr^2\displaystyle\int^{\infty}_0\frac{\cos^3\theta}{z^3}dz\)
となります。
■\(z\)変数の処理
また、\(\tan\theta=\displaystyle\frac{r}{z}\) なので、
\(\displaystyle\frac{1}{z}=\frac{\sin\theta}{r\cos\theta}\) ; \(\displaystyle\frac{1}{z^3}=\frac{\sin^3\theta}{r^3\cos^3\theta}\) から、
\(H=nIr^2\displaystyle\int^{\infty}_0\cos^3\theta・\frac{\sin^3\theta}{r^3\cos^3\theta}dz\)
\(H=nIr^2\displaystyle\int^{\infty}_0\frac{\sin^3\theta}{r^3}dz\)
となります。
■\(dz\)の処理
さらに、\(\tan\theta=\displaystyle\frac{r}{z}\) から、\(z=\displaystyle\frac{r\cos\theta}{\sin\theta}\) としておいて\(\theta\)で微分すると、
\(\displaystyle\frac{dz}{d\theta}=-\frac{r}{\sin^2\theta}\)
となりますので、
\(dz=-\displaystyle\frac{r}{\sin^2\theta}d\theta\)
を適用して、積分区間も置換してやると、
\(H=nIr^2\displaystyle\int^0_{\frac{\pi}{2}}\frac{\sin^3\theta}{r^3}\left(-\frac{r}{\sin^2\theta}\right)d\theta\)
\(H=nIr^2\displaystyle\int^{\frac{\pi}{2}}_0\frac{\sin\theta}{r^2}d\theta\)
■そして本丸へ!
よって、
\(H=nI\displaystyle\int^{\frac{\pi}{2}}_0\sin\theta d\theta\)
\(H=nI\displaystyle \left[-\cos\theta \right]^{\frac{\pi}{2}}_0 d\theta\)
\(H=nI(-0+1)\)
\(H=nI\)
と計算され、気が付くと半径\(r\)に依存しない定数だけが残ってしまいました。
こうなると、\(r\)にどんな値を入れて計算しても、最終的に計算結果として残るのは、いつでも\(nI\)ということになってしまいます。
どうやら本当にコイルの半径に関わらず、コイル内部の磁場はいつでも\(nI\)になるようですね。
ただし一つだけ注意点があります。これは無限に長いソレノイドコイルの場合ですので、有限の長さであれば半径によっても、コイルの端部なのか中央部なのかによっても計算結果が変わってしまいます。
これについての数式変形は、また同じくらいの行数をかけて変形していかないといけなくなりますので、今回は話題にしませんが、計算で確認することはできます。いつかはチャレンジしてみてください。

コメントをお書きください