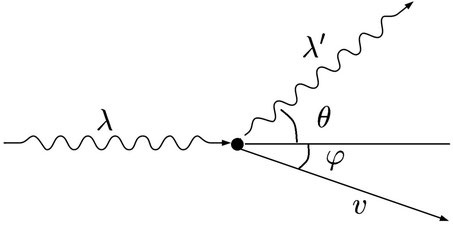
入射X線のエネルギーと運動量
\((E_0,p_0)=(\displaystyle\frac{hc}{λ} , \frac{h}{λ})\)
散乱X線のエネルギーと運動量
\((E_X,p_X)=(\displaystyle\frac{hc}{λ'} , \frac{h}{λ'})\)
散乱電子のエネルギーと運動量
\((E_e,p_e)=(\displaystyle\frac{1}{2}mv^2 , mv)\)
と書けるので、エネルギーと運動量について、それぞれ保存則を立てることにします。
①エネルギー保存則
\(\displaystyle\frac{hc}{λ}=\frac{hc}{λ'}+\frac{1}{2}mv^2\)
②x軸方向の運動量保存則
\(\displaystyle\frac{h}{λ}=\frac{h}{λ'}\cosθ+mv\cosφ\)
③y軸方向の運動量保存則
\(0=\frac{h}{λ'}\sinθ-mv\sinφ\)
ここからの解答指針として、
②③から\(φ\)を消去
↓
①を変形して\(mv\)の形を作る
↓
式を1本化
↓
\(\frac{λ'}{λ}\)と\(\frac{λ}{λ'}\)の形を作る
↓
\(λ'=λ+Δλ\)とおき、近似
という流れで解いていきます。すると、最終的に連立式の解として
\(Δλ=\displaystyle\frac{h}{mc}(1-\cosθ)[m]\)
\(Δλ=2.4×10^{-12}(1-\cosθ)[m]\)
が求まります。
では手順を追って式変形していきましょう。やることは単に連立式を解くだけですので、ここで紹介する方法以外の方法で、自分がやりやすい方法があれば、それでも構いません。
Step1:②③式を1本化
\(\displaystyle\frac{h}{λ}=\frac{h}{λ'}\cosθ+mv\cosφ\)
\(0=\displaystyle\frac{h}{λ'}\sinθ-mv\sinφ\)
より、\(φ\)の項とそれ以外の項を分けておく
\(\displaystyle\frac{h}{λ}-\frac{h}{λ'}\cosθ=mv\cosφ\)
\(\displaystyle\frac{h}{λ'}\sinθ=mv\sinφ\)
それぞれ2乗する
\(\displaystyle\left(\frac{h}{λ}-\frac{h}{λ'}\cosθ\right)^2=m^2v^2\cos^2φ\)
\(\left(\displaystyle\frac{h}{λ'}\sinθ\right)^2=m^2v^2\sin^2φ\)
辺々足すと
\(\displaystyle\left(\frac{h}{λ}-\frac{h}{λ'}\cosθ\right)^2\)+\(\displaystyle\left(\frac{h}{λ'}\sinθ\right)^2\)=\(m^2v^2\cos^2φ\)+\(m^2v^2\sin^2φ\)
\(\displaystyle\left(\frac{h}{λ}-\frac{h}{λ'}\cosθ\right)^2\)+\(\displaystyle\left(\frac{h}{λ'}\sinθ\right)^2\)=\(m^2v^2\)
\(\displaystyle\frac{h^2}{λ^2}-2\frac{h^2}{λλ'}\cosθ+\frac{h^2}{λ'^2}\cos^2θ\)+\(\displaystyle\frac{h^2}{λ'^2}\sin^2θ\)=\(m^2v^2\)
\(\displaystyle\frac{h^2}{λ^2}-2\frac{h^2}{λλ'}\cosθ+\frac{h^2}{λ'^2}=m^2v^2\) ―――④
これでまず運動量保存則を一本化できました。
これを④式としておきます。
この④式は、運動量保存則を成分に分けて導出しましたが、実際は余弦定理を用いて、直接的に求めることもできます。
Step2:①式を変形しておく
\(\displaystyle\frac{hc}{λ}=\frac{hc}{λ'}+\frac{1}{2}mv^2\)
\(\displaystyle\frac{hc}{λ}-\frac{hc}{λ'}=\frac{1}{2}mv^2\)
より、両辺\(2m\)倍して、左辺の\(hc\)はくくっておきましょう。
\(2mhc\left(\displaystyle\frac{1}{λ}-\frac{1}{λ'}\right)=m^2v^2\) ―――⑤
これを⑤式としておきます。すると④式との統合ができそうですね。
Step3:④式と5式を一本化
\(\displaystyle\frac{h^2}{λ^2}-2\frac{h^2}{λλ'}\cosθ+\frac{h^2}{λ'^2}=m^2v^2\) ―――④
\(2mhc\left(\displaystyle\frac{1}{λ}-\frac{1}{λ'}\right)=m^2v^2\) ―――⑤
より、
\(\displaystyle\frac{h^2}{λ^2}-2\frac{h^2}{λλ'}\cosθ+\frac{h^2}{λ'^2}=2mhc\left(\frac{1}{λ}-\frac{1}{λ'}\right)\)
×\(\frac{1}{h^2}\)
\(\displaystyle\frac{1}{λ^2}-2\frac{1}{λλ'}\cosθ+\frac{1}{λ'^2}=2\frac{mc}{h}\left(\frac{1}{λ}-\frac{1}{λ'}\right)\)
通分
\(\displaystyle\frac{1}{λ^2}-2\frac{1}{λλ'}\cosθ+\frac{1}{λ'^2}=2\frac{mc}{h}・\frac{λ'-λ}{λλ'}\)
×\(λλ'\)
\(\displaystyle\frac{λλ'}{λ^2}-2\cosθ+\frac{λλ'}{λ'^2}=2\frac{mc}{h}(λ'-λ)\)
約分
\(\displaystyle\frac{λ'}{λ}\)\(-2\cosθ+\)\(\displaystyle\frac{λ}{λ'}\)\(=2\displaystyle\frac{mc}{h}(λ'-λ)\) ―――⑥
Step4:λ'の置き換え
ここで、λ'を、元のλと比べて微小量だけ増えた量であると解釈して、
λ'=λ+Δλ とおくと、これの両辺をλで割った値は
\(\displaystyle\frac{λ'}{λ}=1+\frac{Δλ}{λ}\)
これはそのまま使えそうです。一方で、その逆数は
\(\displaystyle\frac{λ}{λ'}=\left(1+\frac{Δλ}{λ}\right)^{-1}\)
これは、いま\(Δλ<<λ\)であるから、
\((1+x)^n≒1+nx\)の近似を用いて、
\(\displaystyle\frac{λ}{λ'}=1-\frac{Δλ}{λ}\)
これをそれぞれ⑥式に代入しましょう。
Step5:Δλを求める
\(\displaystyle\frac{λ'}{λ}\)\(-2\cosθ+\)\(\displaystyle\frac{λ}{λ'}\)\(=2\displaystyle\frac{mc}{h}(λ'-λ)\) ―――⑥
より、近似して
\(\displaystyle\left(1+\frac{Δλ}{λ}\right)\)\(-2\cosθ+\)\(\left(1-\displaystyle\frac{Δλ}{λ}\right)\)\(=2\displaystyle\frac{mc}{h}(λ'-λ)\)
よって、
\(2-2cosθ=2\displaystyle\frac{mc}{h}(λ'-λ)\)
\(λ'-λ=\displaystyle\frac{h}{2mc}(2-2\cosθ)\)
\(λ'-λ=\displaystyle\frac{h}{mc}(1-\cosθ)\)
となります。
\(m=9.1×10^{-31}[kg]\)
\(c=3.0×10^8[m/s]\)
\(h=6.6×10^{-34}[J・s]\)
を代入して計算すると、
\(λ'-λ=2.4×10^{-12}(1-\cosθ)\)
となります。
これを全部解こうと思うと、相当な計算力と時間がかかるので、入試では出題者も扱いづらいわけです。なので、キーになる部分が空欄にされた状態で、式変形の流れだけをつかませるような出題しかできないんじゃないでしょうか。
