
Atwoodの器械
イギリスの数学者\(George Atwood\)(アトウッド)は1784年、\(Newton\)の第二法則を検証するために、一定の加速度を作り出せる装置を開発しました。当時、正確なストップウォッチもなく、\(Newton\)の法則を検証するためには重力加速度の大きさ\(9.8m/s^2\)はあまりにも大きく、ゼロコンマ何秒の世界を正確に判定できる実験器具はありませんでした。\(Atwood\)はそんな時代背景の中で、重力加速度の大きさを精密に測定する器械を開発したのです。
この器械の原理は非常に単純で、簡略化して説明すると、図のように定滑車の左右におもりをつけただけの装置です。あとで見ますが、こうすることで一定の大きさの重力加速度を自由に作り出せることができるので、火星の重力だろうと、月の重力だろうと容易に設定することができるわけです。
あまりにも精密な器械であったため、化学電池を開発した\(Volta\)(ボルタ)でさえも衝撃を覚えたそうです。
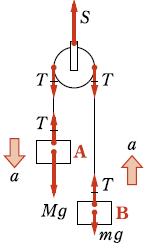
Atwoodの器械への運動方程式
質量5.0kgの物体Aと質量3.0kgの物体BをそれぞれAtwoodの器械につるしたとします。このとき、
(1)加速度aはいくらか
(2)物体をつるしている張力Tはいくらか
(3)滑車をつるしている張力Sはいくらか
を求めてみようと思います。滑車と糸の重さや摩擦、空気抵抗はないものとします。重力加速度の大きさは\(9.8m/s^2\)とします。
余談ですが、滑車に重さがあると、慣性モーメントと言われるものがはたらいてしまい、滑車が回転しにくくなりますので、張力Sはもちろんのこと、実はaもTも変化してしまいます。なので、滑車をつるしている糸の張力Sを問うていなくても滑車の質量はないものと記述している問題は多いです。
まず作図をします。物体A,Bともに重力を作図し、それぞれ上向きの張力\(T\)を書き入れましょう。
次に加速度の向きを設定します。問題文に、物体Aを降下させて、と書いてあるので、物体Aの加速度を下向きに、物体Bの加速度を上向きに設定することにします。
(1)
物体Aの運動方程式は
\(Ma=Mg-T\)
\(5a=5×9.8-T\)
\(5a=49-T\)
物体Bの運動方程式は
\(ma=T-mg\)
\(3a=T-3×9.8\)
\(3a=T-29.4\)
なので、辺々を足して
\(8a=49-29.4\)
\(8a=19.6\)
∴
\(a=\displaystyle \frac{19.6}{8}\)
\(a=2.45\)
\(a≒2.5[m/s^2]\)
となります。重力加速度の大きさが\(9.8m/s^2\)であることと比べると、ずいぶん小さな値ですね。火星より少し小さくて、月よりは少し大きいくらいの重力に相当する値です。\(Atwood\)の器械で運動している間は、この加速度は途中では変わりません。ずっと一定の加速度で実験が行われます。
(2)
物体Bの運動方程式へ(1)の加速度を代入すると
\(3×2.45=T-29.4\)
\(7.35=T-29.4\)
\(T=29.4+7.35\)
\(T=36.75\)
\(T≒37[N]\)
となります。これは計算して確かめてみるといいですが、3.75kg分の重力に相当します。なので、物体Aについては、下に5.0kg分、上に3.75kg分の力がかかり鉛直下向きに動く、物体Bについては、下に3.0kg分、上に3.75kg分の力がかかり鉛直上向きに動く、ということになるので矛盾なく説明がつく値です。
(3)
滑車に注目すると、滑車を上向きに引く糸は1本で、下向きに引く糸は2本あることに気づきます。
ここから、
\(S=2T\)
\(S=2×36.75\)
\(S=2×36.75\)
\(S=73.5\)
\(S=74[N]\)
となります。これはmgの計算で確かめると分かりますが、何と驚くことに7.5kg分の重力にしかならないんですね。5.0kgと3.0kgのおもりをつるして動かした結果、両方のおもりを足した8.0kgよりも小さな力が全体にかかることになるんです。雑な説明をすると、8.0kgのうち一部が落ちているから軽くなっている、と解釈するんです。一物体の運動方程式のときも同じでしたよね。糸につられた100Nの物体が静止していれば張力は100Nですが、下向きに加速しているときは張力は100Nより小さな値になります。それと同じことが起きているわけです。
この事実は知っておいた方がいいですよ。計算していって、途中で初めてこの事実と直面した高校生は、どこかに計算ミスがあるんじゃないかと、徹底的に計算をやり直しますが、どこにもミスがでてこない。なんて言ったって事実ですから。
Atwoodの器械は運動中のときに限って、おもりの合計値よりも小さな力が天井にかかるんです。
