浮力
物体が、流体(気体や液体)の中にあるとき、浮き上がろうとする力のことを浮力といいます。例えば、水に沈めた浮き輪や、空気中で膨らませた熱気球のようなものをイメージすると、浮き上がっていく姿がわかるかと思います。
この浮力の大きさについては歴史が古く、古代ギリシャの数学者アルキメデスが紀元前3世紀頃にはすでに原理の説明をしています。有名な「アルキメデスの原理」と言われるものです。
ふちギリギリまで目いっぱい水が入った水槽を用意します。ここに物体を沈めると、水があふれますね。そして物体は水に沈められていますので、浮力が生じています。この浮力が一体、何\(N\)なのか。それは、あふれた水の重さをはかってやると分かります。
あふれた水の重さが仮に\(2N\)であったとすると、この物体にかかっている浮力も同じ\(2N\)になっている、ということをアルキメデスは発見しました。
なんでそんなことが起こるかって?それは分かりません。分かりませんが、なるものはなるんです。なので、アルキメデス的には浮力に関する原理の説明として、
「物体に生じる浮力は、その物体が押しのけた流体(気体や液体)の重さと等しい」
としました。これがアルキメデスの原理です。
原理と法則
なぜ、アルキメデスの原理なのか。という余談を少し話しておこうと思います。
原理、というのは、なぜそうなるのかいまいち分かっていない、科学的に説明ができない、という物理的なルールに付けられる言葉です。アルキメデスの原理のほか、仕事の原理や、てこの原理、現代でも光速度不変の原理、といったものがあります。
科学(サイエンス)というものは、何かが判明したり新しい発見があった上で先に進むイメージが強いかと思いますが、必ずしもそうとは限りません。なぜそうなるか分からないことが残っているけれど、事実は事実として、なるものはなる、何回もなる、ということが明らかなとき、例外探しをせずに、まあ成立することを前提に話を進めてみようじゃないか、という立場に立つ科学者も多いわけです。
「○○が成立するとしたら、□□である」、ということです。じゃあ成立しないこともあるのか、ということになりますよね。結論を言うと、そういうこともあります。そのときは、「○○が成立しないときは、□□である」、という方向に科学を発展させてしまいますので、「○○が成立するとしたら、□□である」、の部分は理論ごと生き残ってしまいます。条件が制約されるだけで、理論ごと破綻することは案外少ないものです。
とにかく、なんでそうなるかよくわからないけれど、なることを前提に話を進めてみましょう、というスタンスで前提に置かれる条件を「原理」といいます。
法則は、原理と違い、きちんと説明がつくものを言います。慣性の法則、作用反作用の法則、オームの法則など、いろいろありますが、いずれも科学的に論理的に説明がつけられたものが「法則」という名前をもらえます。
浮力の大きさ
浮力がどこからやってくるかは当時分かっていませんでしたが、あふれた水の重さをはかることは簡単です。皆さんはすでに現代科学の時代に生きていますので、1600年代に活躍した\(Newton\)の物理を使って、測定なしで浮力の大きさを考えることができます。
あふれた水の重さを\(W\)とすると、水にかかる重力の大きさは
\(W=mg\)
と書くことができます。ここでほとんどの人が忘れ去ってしまっている、中学理科の密度の公式を思い出します。
\(密度=\displaystyle\frac{質量}{体積}\)
という関係があります。高校物理っぽく、それぞれの物理量を全て文字で置き換えることにします。
密度を\(\rho\)(ロー)、質量を\(m\)、体積を\(V\)としてやると、
\(\rho=\displaystyle\frac{m}{V}\)
となりますので、ここから式変形して、
\(m=\rho V\)
としておきます。これを水の重力の式に代入すると、
\(W=mg=\rho V g\)
となりますが、この水の重さが浮力の大きさそのものですので、浮力の大きさを\(F\)とすると
\(F=\rho V g\)
とすることができます。
▼浮力
\(F=\rho V g\)
\(F[N]\):浮力
\(\rho[kg/m^3]\):液体の密度(※物体の密度ではない)
\(V[m^3]\):物体の体積(※あふれた液体の体積と同じ)
\(g[m/s^2]\):重力加速度
浮力の発生
古代ギリシャの時点では「原理」だった浮力ですが、少し時代が下ると、浮力の発生由来が水圧からくるものだということが比較的簡単な計算で説明付くことが判明しました。なぜか「法則」に格上げはされませんでしたが、今では、浮力の発生理由を、きちんと数式で説明することができます。
この説明方法については、入試や模試でも触れられることがありますので、たどってみましょう。
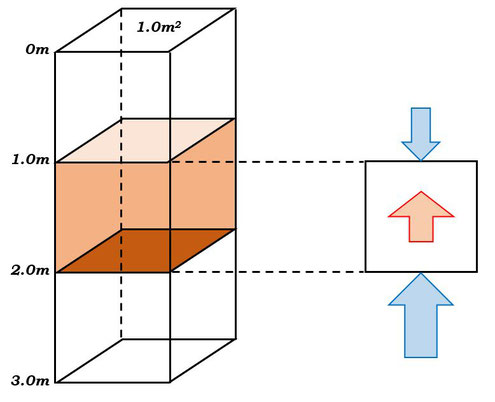
深いプールがあったとします。そのプールの水を\(1.0m^2\)の面積分だけ切り出して、図のように直方体として描いたとします。
この直方体の真ん中あたりのところに、\(1\)辺\(1m\)のブロックがあることにしますね。
水圧は、深いほど強い圧力になりますので、この”箱”の上面にかかる水圧と下面にかかる水圧には違いがあります。
箱の上面には水深\(1m\)の水圧がかかります。水圧の大きさの概算としては、\(1cm\)あたり\(1hPa\)つまり\(100Pa\)ですので、水深\(1m\)なら、約\(100hPa\)の水圧がかかっています。
箱の下面は、水深\(2m\)ですので、およそ\(200hPa\)の水圧がかかっていることになります。
箱の側面にも深さごとに異なる水圧がかかっていますが、左右が逆向きですので、すべて打ち消しあって、特に浮力を考えるときには関係ない量になりますので、省略しました。
さて、図に示した通り、上面にかかる水圧と下面にかかる水圧の大きさに違いがありますので、その差の分として、上向きに物体を押し上げようとする圧力が生じています。これが由来となって生じる、上向きの力が浮力です。
浮力の大きさの計算
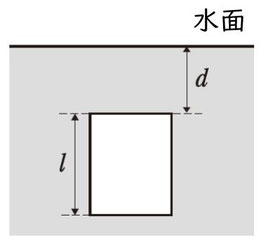
図のように、高さ\(l\)で、断面積\(S\)の直方体を、上面が水深\(d\)となるように沈めたとします。このとき、直方体が受ける浮力を具体的な数式で導出してみようと思います。
水圧の公式は\(\rho hg\)ですが、大気圧も含めた水圧の公式は \(p=p_0+\rho hg\) なので、\(h\)の部分を今の設定のように深さ\(d\)という文字に変えて考えます。
\(p=p_0+\rho hg\) より
\(p_{上面}=p_0+\rho dg\)
\(p_{下面}=p_0+\rho (d+l)g\)
\(p_{上面}\)より\(p_{下面}\)の方が深いところですので、その分水圧も強くなっています。\(p_{下面}\)の方が大きい値なので、\(p_{下面}\)から\(p_{上面}\)をひきましょう。 ただし、単に水圧差を求める問題なのではなく、力の差となっているので、
\(F=PS\) より
\(F_{上面}=p_{上面}S={p_0+\rho dg}S\)
\(F_{下面}=p_{下面}S={p_0+\rho (d+l)g}S\)
としておいてから、
\(F_{下面}-F_{上面}={p_0+\rho (d+l)g}S-{p_0+\rho dg}S\)
\(=p_0S+\rho dgS+\rho lgS-p_0S-\rho dgS\)
\(=\rho lgS\)
となります。ここで、\(lS\)は、高さ×底面積で示される直方体の体積ですので、\(V\)と書き換えてやると、結局浮力\(F\)は、
\(F=\rho V g\)
となりました。
