熱電子
さて、ようやく数式が登場します。電子の比電荷を求める式を導出してみようと思います。まずは実験器具の仕組みから話を進めます。
金属を高温にすると、金属内部の自由電子が激しく運動して、その一部が金属の表面から外部に飛び出すことがあります。このような電子を熱電子と呼びます。熱電子を人工的に発生させてとり出す装置を電子銃といいます。電子銃を使うと、放出される陰極線(電子)の初速度を自分で設定することができるので、後々の計算で利用することが出来ます。
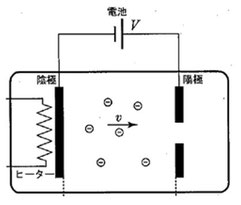
電子の初速度の計算
では、電子銃で飛び出す電子の初速度はいったいいくらになるのかを考えていきましょう。
まず、図のように電子銃を組み立てて、電圧Vを極板間に加えます。余談ですが、正式には電圧をかけることを、「電圧を印加(いんか)する」といいます。
極板に電圧を加えると、負の電子は負の極板から反発し、正の極板に引き寄せられていくので、徐々に加速していきます。
最初、負の極板の表面に初速度0の電子があったとすると、電圧によって加速された電子は正の極板に到達するころには運動エネルギーを持ちます。このエネルギーの大きさは全て極板が電子にした仕事の大きさと等しいので、
\(\displaystyle\frac{1}{2} mv_0^2=eV\)
の関係が成り立ちます。ここから、電子が正の極板に到達したときの速度は
\(v_0=\displaystyle\sqrt{\frac{2eV}{m}}\)
と計算できます。図のように、正の極板の真ん中に穴をあけておけば、加速された電子が速度\(v_0\)で穴から放出されて電子銃として機能します。
ちなみに、この\(v_0\)はみなさんが実験するとしたら便利だ、という現代科学の立場から導出した式であって、トムソンの時代には電子の質量mや電子の電気量eはまだ知られていませんから、この方法では\(v_0\)は分かりません。
むしろ、今からなぞっていく科学史では、この\(m\)や\(e\)をどうやって求めていくのか、という話なので\(v_0\)が式に現れないように調整しないといけませんね。
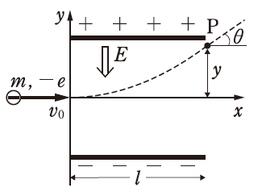
陰極線に電場を加える
コンデンサーの極板間のような一様な電場\(E\)の中に電子が初速度\(v_0\)で入り込んできたと考えます。すると、ちょうど重力がはたらく空間中で物体が水平投射されるのと同じように放物線運動をします。
重力の場合は\(mg\)と考えるところを、電場の場合は\(qE\)と考えるところに文字や単位の違いがありますが、あとは単なる水平投射の問題と同じなので、使う文字にだけ注意をすれば、特段小難しく説明する必要はないでしょう。実際に問題を解きながら確認していきましょう。
例題
図のように、長さ\(l\)の領域に\(-y\)方向の一様な電場\(E\)を加える。この電場と直角に、質量\(m\)、電気量\(-e\)の電子を\(x\)方向に初速度\(v_0\)で電場内に入れた。
(1) 電場内を電子が通りぬける時間\(t\)を求めよ。
(2) 電場内での電子の加速度\(a\)の大きさと向きを求めよ。
(3) 電場を通りぬけた点\(P\)での\(y\)座標(図の\(y\))を求めよ。
(4) (3) の点\(P\)で、軌道と\(x\)軸がなす角度\(θ\)の正接(\(tanθ\))を求めよ。
[解答]
(1)
速度のx成分は\(v_0\)で一定だから、\(x=v_xt\)の関係式より\(l=v_0t\)となる。
よって\(t=\frac{l}{v_0} \)
(2)
電子は\(+y\)方向に静電気力を受ける。
\(F=qE\)の関係式より、運動方程式は
\(ma=eE\)
よって
\(a=\frac{eE}{m}\)
向きは\(+y\)方向
(3)
\(y\)方向の運動について、等加速度運動の式 \(y=v_{0y}t+\frac{1}{2}at^2\) を用いると
\(y=\displaystyle\frac{1}{2}at^2\)
\(y=\displaystyle\frac{1}{2}・\frac{eE}{m}・(\frac{l}{v_0})^2\)
\(y=\displaystyle\frac{eEl^2}{2mv_0^2}\)
(4)
点Pでの速度の\(x\)成分は\(v_x=v_0\)
\(y\)成分は\(v_y=v_{0y}+at\)の式より
\(v_y=at\)
\(v_y=\displaystyle\frac{eE}{m}・\frac{l}{v_0} \)
よって
\(tanθ=\displaystyle\frac{v_y}{v_x}\)
\(tanθ=\displaystyle\frac{\frac{eEl}{mv_0}}{v_0}\)
\(tanθ=\displaystyle\frac{eEl}{mv_0^2}\)

ちなみに、このあと陰極線はスクリーン上のどの位置に現れるかを聞かれる場合は、もはや極板の外に出てしまった陰極線は真 っすぐ進むだけですから、三角比を使って図形的に求めましょう。
\(Y=y+Ltanθ\)と書け、前問で\(y\)も\(tanθ\)も分かっているので、
\(Y=\displaystyle\frac{eEl^2}{2mv_0^2}+\frac{eELl}{mv_0^2}\)
\(Y=\displaystyle\frac{eEl(l+2L)}{2mv_0^2}\)
としてしまえば、あまり複雑な計算なく導出ができます。

陰極線に磁場を加える
陰極線に電場を加えることでスクリーンの座標\(Y\)に向かって陰極線が曲がっていきますので、\(Y\)を測定して未知数の\(m\)や\(e\)を求めようと思います。
\(l\)や\(L\)は実験器具の長さですので測定は簡単にできるでしょうし、極板間の電場\(E\)も\(V=Ed\)を用いれば回路の電圧\(V\)と極板間隔\(d\)から分かります。
ところが一つ積み残していることがありますね。\(v_0\)が未知数のままです。当時の科学力では、陰極線の初速度は\(m\)や\(e\)からは導出できませんので、別の方法を考えます。電場を加えるのをやめて、磁場を加えることにします。
科学史をひもとくと、実際には陰極線の性質として、磁場で曲がることは早期に広く知られていました。そこにトムソンが登場し、陰極線が電場でも曲がることを突き止めたので理論に進展が見られたわけですが、今回は電場の話を先にしてから磁場の話を後に回しました。その方が計算も楽になるし、理解もしやすいからです。
トムソンはきっと苦心しながら実験したんでしょうが、現代人の我々が「苦心」の部分まで再現する必要はありません。簡単にできるなら簡単にできる方法で学んでいきましょう。
極板に電場だけを加えると陰極線は放物線運動をしてしまいますが、電場だけではなく磁場も同時に加えると、ローレンツ力を受けるので、陰極線は再び極板内を真っすぐ進むことが出来ます。
ここで少しだけ用語の復習をします。静電気による力のことをクーロン力とよび、\(F=qE\)で表します。電流や電荷が磁場中で受ける力のことをローレンツ力とよび、その力の向きを表す法則をフレミングの左手の法則、もしくはローレンツの右手の法則とよび、力の大きさは\(F=IBl\)もしくは\(F=qVB\)で表します。
今回、電場と磁場を同時に加えて陰極線が直進するということは、クーロン力とローレンツ力がつり合っている条件を作ればいいわけです。
つまり、\(eE=ev_0B\)より、\(v_0=\frac{E}{B}\)となり、とても シンプルに陰極線の初速度を決めることができます。 これで未知数は全て消えました。こうして得られた物理量\(\frac{e}{m}\)を電子の比電荷とよびます。
実験の結果、比電荷は極板に用いる金属の種類や真空放電管内の気体の種類によらず、常に\(1.76×10^{11}C/kg\)という値になることが分かりました(1897年)。
