熱容量と比熱
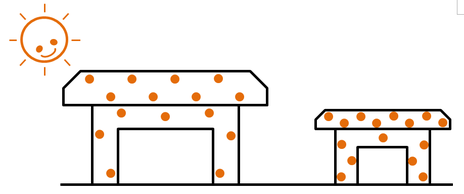
大きい建物と小さい建物があって、どちらも太陽がサンサンと熱を加えているとします。この建物2つを比べたときに、どちらの方が断熱効果が高いでしょうか。
断熱効果が高いということは、どういうことでしょうか。
建物が熱を吸収していき、吸収しきれなくなってついに内側の部屋にまで太陽の熱が染み出すようになったら、断熱の性能は使い果たされていると考えることにします。
イラストのように、大きい建物と小さい建物に熱がため込まれているイメージをします。●1つが同じ量の熱エネルギーだと考えてください。直感的に理解できるのは、建物は大きければ大きいほど、熱をためるのに有利だということです。
真夏の車の中に、締め切った状態で入っていると、すぐに熱がこもりますが、家くらいのサイズなら日が昇ったあと、冷房なしでも数時間は耐えらえます。体育館やドームくらいのサイズなら、熱がこもるまで、さらに時間がかかるでしょうね。
このように、物体は熱をたくわえるための容器の役割があります。このときの容量のことを、熱容量といいます。蓄えられる熱量の総量は、熱容量×温度で計算できます。
しかし、断熱効果が高い建物は、はたして本当に大きい建物だと言っていいのでしょうか。大きい建物の方が断熱性能を測るのに有利ですから、真に断熱効果が高いのかどうかは、同じ大きさで比べてやらないと意味がなさそうです。
そこで、同じ基準として、「1gあたり」という共通指針を作ることにします。このときの熱容量のことを比熱といいます。比熱を使えば、真に物質の性質を比較することができそうですね。質量×比熱を計算すると、もとの熱容量に戻ります。
▼熱容量と比熱
熱容量:物体の温度を1K変化させるのに必要な熱量
比熱:物体1gの温度を1K変化させるのに必要な熱量
熱量\(Q[J]\)、質量\(m[g]\)、比熱\(c[J/(g・K)]\)、熱容量\(C[J/K]\)、温度変化\(\Delta T\)として
\(Q=C\Delta T\)
\(Q=mc\Delta T\)
\(C=mc\)
熱平衡

高温物体と低温物体を接触させて、しばらく時間をおくと、やがて同じ温度になりました。
このとき、熱は必ず高温の物体から低温の物体に進みますが、温度が等しくなったとき(熱平衡という)、人間には認識できないほど小さな温度差があるはずです。
ごくわずかにでも温度差があれば、高温の物体側から低温の物体側に熱が移動し、高低が逆転すれば熱の移動も逆転するので、遠目から見れば人間には温度が等しくなって変化がないように見えます。しかし、実際は左右にしきりに熱が移動しあっている状態が熱平衡の状態です。
熱量保存則
さて、質量\(m_1\)、比熱\(c_1\)、温度\(t_1\)の高温物体と、質量\(m_2\)、比熱\(c_2\)、温度\(t_2\)の低温物体とを接触させて熱平衡に到達したとき、どのくらいの熱量が移動し、最終的に何℃になったのでしょうか。
これを考えるときに使う法則を「熱量保存の法則」と言います。熱量とは熱エネルギーのことなので、エネルギー保存則のうちの、熱力学バージョンの法則ということですね。単位はエネルギー単位\([J]\)での意味を持つ式です。

高温物体が失った熱量は、すべて低温物体が受け取るので、それぞれの熱量を計算すると、その値は等しい量になりますよ、というのが熱量保存則の考え方です。
高温の物体が失う熱量は
\(Q=mc\Delta T\) より
\(Q=m_1c_1\Delta T\)
ここで、\(\Delta T=t_1-t\)となります。大きい値から小さい値を引き算すると求まるわけですが、今設定している温度は、高温物体が\(t_1\)、低温物体が\(t_2\)、熱平衡のときの温度が\(t\)となっていますので、大小関係順に並べると、\(t_2<t<t_1\)の順番になっています。
図を見ると明確になりますが、温度差の部分が、どの文字で表現されるのかを注意してください。さて、つづけましょう。
低温の物体が失う熱量は
\(Q=mc\Delta T\) より
\(Q=m_2c_2\Delta T\)
ここでの温度変化は、\(\Delta T=t-t_2\)になります。同じく大小関係に注意して書くと、添え字が入れ替わった形になってしまっていますので、気をつけてください。
結局、
\(m_1c_1(t_1-t)=m_2c_2(t-t_2)\)
という形になります。ここに、問題文で与えられる値を代入できさえすれば、求めたい文字について解き進めることができますね。たいがいは\(t\)を求める問題であることが多いので、それ以外の値は問題文か図のどこかから読み取ることができるように作問されていると思います。
▼熱量保存則
\(m_1c_1(t_1-t)=m_2c_2(t-t_2)\)
