平均の速度
物体が移動するとき、必ずしも同じ速度で移動しているとは限りません。途中で加速したり減速したり、場合によっては一部の区間だけ戻ってきているかもしれません。この間の速度の変化を一切考慮せずに、最終的に、何秒間でどのくらい移動したのか、という情報だけから計算した速度を、平均の速度と言います。
▼ 平均の速度
\(\bar{v} = \displaystyle\frac{Δx}{Δt} = \frac{x_2-x_1}{t_2-t_1}\)
\(\bar{v}[m/s]\):平均の速度
\(Δx[m]\):変位
\(Δt[s]\):移動に要した時間
例えば、東京大阪間300kmを、加速したり減速したりしながら3時間で移動したとすると、
\(300km÷3h=100km/h\)
となるわけです。結局は「距離÷時間=速さ」を計算しているにすぎないので、用語が新しく登場した、というだけの話です。
平均の速度を求める問題が出るときは、必ず、スタートからゴールまでの情報が与えられています。どのくらいの距離離れていて、どのくらいの時間をかけて移動したかを問題から読み取ってやれば計算できますので、読み落としがないようにしましょう。
瞬間の速度
移動中の、ある瞬間の速度を計算しようと思えば、移動に要する時間の間隔を小さくすればいいですね。
例えば、\(1.0s\)から\(2.0s\)までの時間にどのくらい移動したか、ということから速度を計算するところを、\(1.0s\)から\(1.1s\)にすれば、より正確な速度を計算できるわけです。
時間間隔を小さくすればするほど正確な速度が求まりますので、\(1.0s\)から\(1.01s\)、\(1.0s\)から\(1.001s\)、という風に間隔を限りなく0に近づければいいわけです。
ただ、完全に0にしてしまうと、\(0s\)間の移動距離は当然\(0m\)ですから、\(0÷0\)となり、計算が成立しません。数学的には、0に限りなく近づく(けど0ではない)というところが大事です。
このような数的な処理を極限と言い、\(\displaystyle \lim_{ n \to 0 }\)のような記号を使いますが、難しそうなので今は置いときます。
物理ではふつう、変化量を\(Δ\)と書きますが、瞬間の速度のように、ごくわずかな変化量(微小量)を考えるときには、\(Δ\)ではなく、小文字の\(d\)を使います。つまり、瞬間の速度の公式を書く場合は、\(\displaystyle\frac{dx}{dt}\)と書きます。意味は変わらず「距離÷時間」です。
いろんな表現があってややこしいですね。ただ、難しいことをやっているわけではなくて、結局ここまでのところ必要な知識は「速さ×時間=距離」という関係しかやっていません。
ぶっちゃけ、この関係さえ知っていれば問題を解くうえではほぼ何も困ることはありません。「ほぼ」というのは、たまに用語が聞かれることがあるので、そのときに「等速直線運動」とか「平均の速度」とか「瞬間の速度」とかいう用語を答えられるように、用語の意味だけはきちんと知っておかないといけません、ということです。
▼ 瞬間の速度
\(v=\displaystyle\frac{dx}{dt}\)
瞬間の速度のグラフ
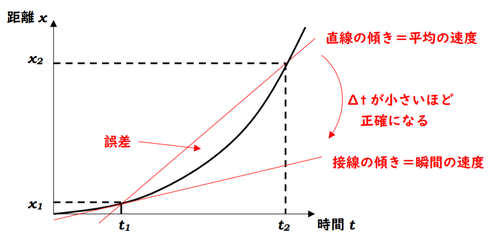
\(x-t\)グラフにおける2点間の直線の傾きは平均の速度を表します。しかしこの間に速度が変わってしまい、正確な速度ではありません。
では正確な速度を求めるためにはどうすればいいのか。
それは、\(Δt\)を小さくすればいいんですね。\(Δt\)を小さくしていくと、やがて接線になります。
\(x-t\)グラフにおける接線の傾きが瞬間の速度を表します。この接線の傾きを求めてやることで、瞬間の速度を求めることができます。
じゃあ接線はどうやって引くのか、ということですが、瞬間の速度を計算させる問題には必ず接線に相当する直線が書かれていますので、自分で書くことはありません。もし、接線が書かれていなければ、それは瞬間の速度を求める問題ではないと解釈してもいいかもしれません。
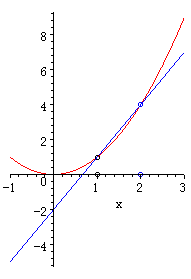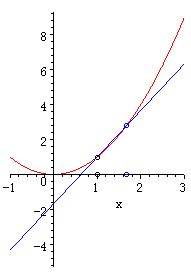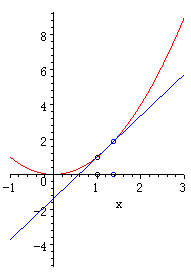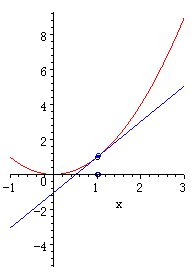
\(Δt\)を小さくしていくと接線になる、という意味が、文字だけではなかなか伝えにくいですので、簡単なgifアニメを付けておきます。
\(1.0s\)から\(2.0s\)の間の速度を求めるよりも、\(1.0s\)から\(1.1s\)、\(1.0s\)から\(1.01s\)と間隔を狭くしていくことで、徐々に正確な速度を求めることができるイメージが持てるでしょうか。
