直線上の相対速度

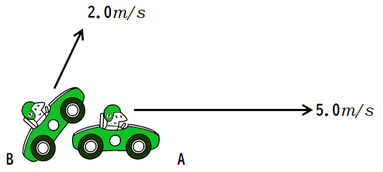
自動車\(A\)と自動車\(B\)がそれぞれ前に速さ\(5.0m/s\)と\(2.0m/s\)で走っています。このとき、\(B\)から見た\(A\)の速さはどのくらいにみえるでしょうか。
\(A\)は前方に走っていますが、\(B\)も同じ向きに走っているので、少しだけ遅く走っているように見えますね。
具体的に数字で計算してみると、\(5.0-2.0=3.0m/s\)の速さで前方に走っているように見えます。
では逆に、\(A\)から\(B\)を見たときは、どのくらいの速さに見えるでしょうか。きっと\(B\)は後ろに\(3.0m/s\)で下がっていくように見えると思います。では実際に\(B\)が後ろ向きに走っているのかというと、そんなことはありませんね。
これも具体的に数字で計算してみると、\(2.0-5.0=-3.0m/s\)となります。
ここで、どうやって計算したのかを考えてみると、「相手の速度」から「自分の速度」を引き算することで、相対速度が求まると分かります。公式で書くと、
\(v_{AB}=v_B-v_A\)
のような、ちょっと難しそうな形をしていますが、要は覚えることとして
相対速度=相手の速度-自分の速度
としてやればいいです。意味が分かっていればわざわざ文字式で覚えなくても、文章のままで覚えるのもありだと思いますよ。
ところが、問題を解こうとすると、一つややこしい事案が判明するんです。上の例でいうのであれば、問題文はいろんなパターンがあって、たとえば、
「Aに対するBの相対速度はいくらか」
「AのBに対する見かけの速度はいくらか」
「AはBに対してどのくらいの速さか」
「Aの速度はBに対していくらか」
のような表現で出題されるわけです。「相手-自分」で計算することはできるのに、肝心の「相手」と「自分」の区別がつかない。これでは、速度の大きさは分かったとしても、それが前方なのか後方なのかが答えられません。
この解決方法として、「に対する」を「から見た」に読み替えることですっきりします。
「Aに対するBの相対速度」を「Aから見たBの速度」と読み替えましょう。同様に、
「Aの、Bから見た速度」
「AはBから見てどのくらいの速度か」
「Aの速度はBから見ていくらか」
こうすれば、どちらが「相手」で、どちらが「自分」かが、ずいぶんとクリアになりますね。見るのは自分ですよ。
平面上の相対速度
ところが平面だと、そう簡単には解決させてくれません。平面での相対速度は「相手-自分」の公式が使えません。
平面での相対速度は
step1:同じところから移動していることにする
step2:「自分」から「相手」へ目線を引く
step3:目線の長さと向きが相対速度を表す
の手順に従って解いていきます。
イラストを貼ってみましたが、このイラスト使わないです。授業のときはこのイラストで説明しますが、文章だとちょっとうまくまとまらないので、違う図で説明しますね。
こっちの図にします。向きの違いが\(90°\)なので、こっちの方が分かりやすそうです。

例題
雨が鉛直に降る中を電車が直線状に一定の速さ\(10m/s\)で進んでいる。雨滴の落下速度を\(10m/s\)とすると、電車内の人が窓から見る雨滴の落下方向と鉛直方向がなす角の大きさを求めなさい。また、雨滴の見かけの速さを求めなさい。
という問題があるとしましょう。これをステップに従って解いてみます。
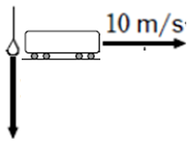
step1:同じところから移動していることにする
ベクトルの始点をそろえる、とも言います。移動している物体は必ずしも同じところから動いているわけではありません。これを無理やり、同じ点からスタートした運動だと読み替えるために、少しだけ図を描き替えておきます。

移動させてみました。電車は前方に\(10m/s\)、雨滴は鉛直下方に\(10m/s\)で進んでいますので、たとえば\(1s\)後の位置を作図したとすれば、それぞれ\(10m\)だけ進んでいることになりますね。
ここでの矢印は、速さを意味する矢印ですが、矢印の長さは距離として解釈することもできますので、速さに応じた長さの矢印を書くことで、この先の理解がラクになりそうです。
この問題ではどちらも\(10m/s\)なので、矢印の長さは揃えておきます。
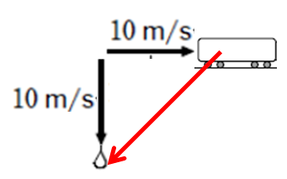
step2:「自分」から「相手」に目線をひく
電車の中に観測者がいますので、電車が「自分」で、雨滴が「相手」です。電車から雨滴に向けて線を引きます。
ここでは説明のために電車や雨滴のイラストが残っていますが、皆さんが実際に解くときには矢印しか書きませんので、ここにきれいな直角三角形が誕生します。
step3:目線の長さと向きが相対速度を表す
ここで図に示した赤い矢印が答えです。これを適切に文章表現すれば解答終了です。
まずは大きさですが、ここに\(1:1:\sqrt{2}\)の直角三角形がありますので、矢印の長さは
\(10×\sqrt{2}\)
\(≒10×1.41\)
\(≒14m/s\)
向きは、落下方向と鉛直方向がなす角で表現してほしい問題だそうなので、\(45°\)となりますね。
どうでしょうか。あとは問題演習をしていく中で理解を深めましょう。
