等加速度直線運動 \(v=v_0+at\)

中学理科では、等速直線運動については計算問題も扱われていましたが、加速したり減速したりする運動に関しては現象だけで終わらせていて、計算問題までは触れられずにいました。高校では、この分野にも切り込んでいきます。
斜面上に小球を静かにおいて、手を離したとします。するとだんだん加速していき、図のように\(1.0s\)後に\(2.0m/s\)、\(2.0s\)後に\(4.0m/s\)という速さの変化があったとします。
このときに、速さがだんだんと速くなるのは直感的にも理解できますが、具体的にどのくらい速くなっていっているのかを決めようと思います。図を見てください。速さがどのくらい増えているかを赤文字で示しました。
速さはランダムな値で増えているわけではなく、\(1.0s\)ごとに\(+2.0m/s\)になる、しかもその量は途中で変わることなく、ずっと\(+2.0m/s\)のままである。こういうとき、\(+2.0m/s\)のように\(1s\)ごとに速くなる割合のことを加速度といい、この加速度がずっと等しい運動のことを等加速度運動といいます。
ここではさらに、運動が直線状であるので特段、等加速度直線運動と呼びます。
等加速度運動には、等加速度円運動というものもあって、物理基礎ではなく専門の物理の単元で学びます。なので、等加速度運動のうち、直線運動に絞って考えていますよ、ということで、等加速度直線運動の方を重要用語として知っておきましょう。
さて、見てのとおり、\(1s\)間でどのくらい速くなったかが加速度のルールなので、加速度は
\(a=\displaystyle\frac{v}{t}\) より
\(v=at\)
となります。
しかし、これは小球が最初に動いていなかった前提で表される式であって、一般的ではありません。物体は最初に動いているかもしれません。

図のように、時間の基準を変えてみます。動き出す瞬間ではなくて、動いて少しだけ経過してからストップウォッチを動かしたというイメージですね。
加速度は同じく\(2.0m/s^2\)とならなければいけないはずです。ところが、例えば\(3.0s\)後の速度から加速度を求めてみると、
\(v=at\) より
\(8.0=a×3.0\)
\(a=\displaystyle\frac{8}{3}\)
となり、\(2.0m/s^2\)ではない値が出てしまいます。
どこに考え方の違いがあるのか。こんどは逆に、加速度\(2.0m/s^2\)が分かっていることとして\(3.0s\)後の速度を計算してみます。
\(v=at\) より
\(v=2.0×3.0\)
\(v=6.0m/s\)
となりました。おかしいですね。\(8.0m/s\)が出ないといけないはずです。
実は、ここで計算した\(6.0m/s\)という値は、\(3.0s\)での速度を計算したわけではありません。\(3.0s\)間に、最初の時点から、どのくらい速度が増えたか、を計算しています。
\(0s\)の時点ですでに\(2.0m/s\)の速度がありますので、これを追加すれば、
\(v=2.0+6.0\) より
\(v=8.0m/s\)
となってくれます。
つまり、物体が最初に静止していようと運動していようと関係なく速度を求めようと思えば、最初の速度+加速する分の速度を考える必要があります。
こうして、速度の公式は加速度\(a\)を用いて、最初の速度(初速度)を\(v_0\)と表記すれば、
\(v=v_0+at\)
となります。
等加速度直線運動 \(x=v_0t+\frac{1}{2}at^2\)
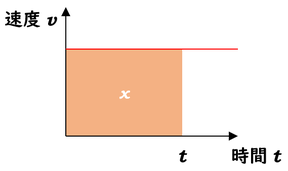
速度を縦軸に、時間を横軸に取ったグラフを\(v-t\)グラフといいます。
等速直線運動を思い出してみると、移動距離は\(x=vt\)でしたので、グラフでいう面積(\(v×t\))を計算すれば移動距離を計算したことになります。
この考え方は等速直線運動に限らず、一般的に速度が自由に変化していようが、面積を求めさえすれば移動距離を計算することができるんです。
(復習 物基4 等速直線運動)
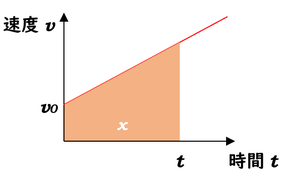
そこで、等加速度直線運動の\(v-t\)グラフでも面積計算から移動距離(変位)を計算してみようと思います。
結論から言えば、図の面積を求めて終了です。問題は、それをどうやって導出しているのか、ということですね。
まずグラフの形ですが、等加速度直線運動は、一般的には時刻\(0s\)で、すでに初速度\(v_0\)で動いている前提とします。動いていなければ\(v_0=0\)としてしまえばいいですので、ここでは値を持つことにしておきます。
で、加速していますので、速度がだんだんと増えます。グラフの形は一次関数になり、\(y=ax+b\)のように表記するのであれば、\(v=at+v_0\)となります。
物理では、慣例的に切片を先に書きますので、\(v=v_0+at\)となり、前に説明した公式と同じになります。
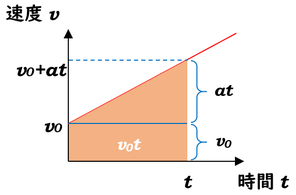
グラフの直線の意味が分かったら、いろんなところに補助線や値を入れてみます。
直線の式が\(v=v_0+at\)なので、横軸が\(t\)のとき、縦軸は\(v_0+at\)となります。
切片の初速度\(v_0\)から横に補助線を引くと、三角形部分と長方形部分に分けることができますが、三角形の高さに相当するところが\(at\)であることさえ理解できれば、あとは自由に面積を計算してやればいいですね。
長方形部分は縦×横でシンプルに\(v_0t\)。三角形部分は底辺\(t×\)高さ\(at÷2\)ということで、
\(\displaystyle\frac{1}{2}at^2\)
となりますので、面積を合計して
\(x=v_0t+\displaystyle\frac{1}{2}at^2\)
となり、これが変位の公式です。
ここでは導出法を扱いましたが、結局最後は、この公式を覚えてさえいればいいというところに落ち着くと思います。
理解できるのが一番いいですが、とりあえず暗記に頼っておいて、のちのち導出のことを考えても間に合いはすると思いますよ。
等加速度直線運動 \(v^2-v_0^2=2ax\)
いま、2公式\(v=v_0+at\)と、\(x=v_0t+\frac{1}{2}at^2\)まで導出しました。
この2式を連立して、\(t\)を消去してみようと思います。
まず\(v\)式を変形して、
\(at=v-v_0\)
\(t=\displaystyle\frac{v-v_0}{a}\)
これを\(x\)式に代入すると、
\(x=v_0・\displaystyle\frac{v-v_0}{a}+\frac{1}{2}a・(\frac{v-v_0}{a})^2\)
\(x=\displaystyle\frac{v_0v-v_0^2}{a}+\frac{1}{2}a・\frac{v^2-2v_0v+v_0^2}{a^2}\)
\(x=\displaystyle\frac{v_0v-v_0^2}{a}+\frac{v^2-2v_0v+v_0^2}{2a}\)
\(x=\displaystyle\frac{2v_0v-v_0^2}{2a}+\frac{v^2-2v_0v+v_0^2}{2a}\)
\(x=\displaystyle\frac{v^2-v_0^2}{2a}\)
\(2ax=v^2-v_0^2\)
となります。この式は、問題文に時間\(t\)が与えられていないときに、裏技レベルでめちゃめちゃ便利な公式です。
▼等加速度直線運動3公式
\(v=v_0+at\)
\(x=v_0t+\displaystyle\frac{1}{2}at^2\)
\(v^2-v_0^2=2ax\)
