弧度法
円運動を学ぶにあたり、数学的な準備として、弧度法を確認しておきましょう。
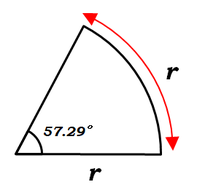
図のように半径\(r\)の円から切り取った扇形があるとします。
このとき、弧の長さがちょうど半径\(r\)と同じになるような扇形は1パターンしか作ることができませんね。
こんな扇形の角度を測ってみると、だいたい\(57°\)くらいになります。

この角度を新しく基準値として、\(1[rad]\)(ラジアン)と定めることにします。
この角度の基準を使って角の大きさを表すことを「弧度法」といいます。
弧の長さ

扇形の中心角と、弧の長さは、比例するので、中心角を\(θ\)倍してやると、弧の長さも\(θ\)倍されて、\(l=rθ\)となります。
▼弧長
\(l=rθ\)
\(l\)と\(r\)は、両方とも単位が長さを表す量なので、\([rad]\)は無次元量だということもわかります。度数法で表した角度も無次元量なので、ちょうどいいですね。
また、1周360°で、弧の長さはちょうど円周\(2\pi r\)になるため、
\(l=rθ\) より
\(2 \pi r =rθ\)
\(θ=2\pi\)
となり、\([rad]\)(ラジアン)は1周あたり\(2\pi\)であることが分かります。
▼1周分のラジアン
\(360°=2\pi[rad]\)
扇形の面積
半径\(r\)の円の面積は\(\pi r^2\)です。中心角の大きさと扇形の面積も比例の関係にありますので、1周\(2\pi[rad]\)のうち、どのくらいの角度の割合だけ扇形があるか、という関係から、扇形の面積を求めることができますね。
扇形の面積を\(S\)とすると、
\(S=\pi r^2 ×\displaystyle\frac{θ}{2\pi}\)
\(S=\displaystyle\frac{1}{2}r^2θ\)
とできますね。
▼扇形の面積
\(S=\displaystyle\frac{1}{2}r^2θ\)
ちなみに、微積を学んだあとであれば、
円周\(2\pi r\) →(rで積分)→ 円面積\(\pi r^2\)
弧長\(rθ\) →(rで積分)→ 扇面積\(\displaystyle\frac{1}{2}r^2θ\)
という関係があることも説明がつくので、この方法で覚える方が早いかもしれませんね。
