円運動６　非等速円運動

　円軌道が鉛直面に置かれるような場合には、円運動は等速とならずに、高さによって速さが異なる運動になります。このような運動は「非等速円運動」と言います。

　非等速円運動の問題が出てきたときには、運動方程式は使えません。なぜなら、この方程式は「等速円運動の運動方程式」だからです。等速でない円運動のときには、そもそも、この式に従う運動にならないわけです。

　では、どんな指針で解けばいいのか。それはとてもシンプルな話です。

　図のように、最下点で勢いをつけて最高点まで飛ばすような運動は、これまでに学習済でした。「力学的エネルギー保存則」を使えばいいですね。しかも、バネが関係するエネルギー問題は少なく、運動エネルギーと位置エネルギーの関係のみの保存則で事足りることが多いです。

▼(復習)力学的エネルギー保存則

　\(\displaystyle\frac{1}{2}mv_1^2+mgh_1=\frac{1}{2}mv_2^2+mgh_2\)

実際にいくつかパターンを見てみましょう。

問：\(AO=\frac{l}{2}\)の長さに釘を打ってある。最高点から物体を落下させ、図の角\(\theta\)の点を通過するときの速さはいくらか。

これは力学的エネルギーで解くパターンの問題ですね。円運動単元ではありませんので、物理基礎の知識を思い出しながら解きましょう。

物体から横に補助線を引くと、青矢印の部分の長さが\(\frac{l}{2}cos\theta\)になるので、\(O\)から最下点までの長さも\(\frac{l}{2}\)であることに注意すると、小球の高さは、

\(h=\displaystyle\frac{l}{2}-\frac{l}{2}cos\theta\)

\(h=\displaystyle\frac{l}{2}(1-cos\theta)\)

となるので、力学的エネルギー保存則より

\(mgl=\displaystyle\frac{1}{2}mv^2+mgh\)

\(mgl=\displaystyle\frac{1}{2}mv^2+mg･\frac{l}{2}(1-cos\theta)\)

\(2gl=v^2+gl(1-cos\theta)\)

\(v^2=2gl-gl(1-cos\theta)\)

\(v^2=gl(1+cos\theta)\)

\(v=\sqrt{gl(1+cos\theta)}\)

というように求めます。

力のつりあいは、どんな感じで出題されて、どんな使い方をするのかも見てみましょう。

問：小球を静かに滑らせると、点Bで面から離れた。\(∠AOB=\theta_0\)とすると、\(cos\theta_0\)はいくらか。

面から離れるとき、糸がたるむとき、のように「離れる」「たるむ」関連の言葉が出てきたら、間違いなく力のつりあいタイプの問題です。

力のつりあいの式を書いておいて、垂直抗力や張力などを\(0\)とする指針で解きます。

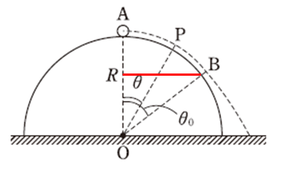
点Bでの力のつりあいを考えるためには、点Bでの遠心力を求めておかなければいけません。ところが、遠心力の式の中には速さが入っていますので、結局、力学的エネルギー保存則で前もって速さを出しておかないといけないことが分かります。

力学的エネルギー保存則で、速さを出したとします。ここの計算過程は省略しますが、点Bでの小球の速さは\(v=\sqrt{2gR(1-cos\theta_0)}\)

これを遠心力の式に代入すると、

\(m\displaystyle\frac{v^2}{R}=m\frac{2gR(1-cos\theta_0)}{R}\)

　　\(=2mg(1-cos\theta_0)\)

重力を分解すると、円の中心を向く成分の大きさ(青矢印)は\(mgcos\theta_0\)となり、遠心力＋垂直抗力の大きさとつり合ったまま落下していきます。

面から小球が離れる瞬間、垂直抗力がついに\(0\)となるので、

重力の中心方向成分＝遠心力　より

\(mgcos\theta_0\)\(=\)\(2mg(1-cos\theta_0)\)

\(cos\theta_0=2-2cos\theta_0\)

\(3cos\theta_0=2\)

\(cos\theta_0=\displaystyle\frac{2}{3}\)

となります。

なんとなく問題を解く流れが見えてきたでしょうか。他にもいろんなパターンがあるので、問題演習を積みながら理解していきましょう。