弾性力
ばねが物体を引いたり押したりする力のことを「弾性力」といいます。
弾性というのは、文字通り、弾力がある性質を意味していて、力を加えるとぷにぷにと形を変えるような性質を言います。
少し詳しく離すと、物体に力を加えても元の形に戻ろうとする力が、弾性力と言われるもので、そのような力が発生する物体のことを「弾性体」と言います。
また、力をいくら加えても、一切形が変わらないものを「剛体(ごうたい)」、力を加えても元の形に戻らずに変形してしまう性質を「塑性(そせい)」といいます。
▼弾性体と剛体
弾性体 力を加えると元の形に戻ろうとするもの
剛体 形が変わらないもの
▼弾性と塑性
弾性 変形させると元の形に戻ろうとする性質
塑性 変形させても元の形には戻らない性質
一つの物体でも、弾性と塑性の両方の性質を持ちますので、たとえば輪ゴムのようなものであれば、ある程度伸ばす間は弾性体としてはたらきますが、伸ばしきれば塑性が強く出て伸びにくくなり、やがて切れます。
この分野では、塑性や破断の話は置いといて、弾性領域だけを扱います。
フックの法則
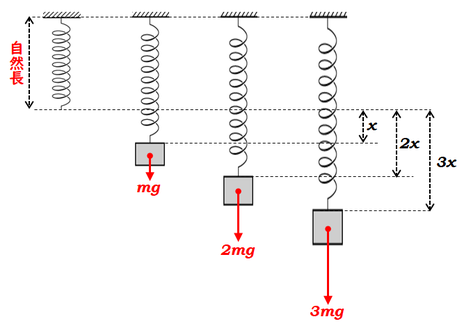
ばねに何もつけない状態でも、ばねそのものには長さがあります。この長さのことを、自然な状態での長さ、という意味で「自然長(しぜんちょう)」といいます。
自然という言葉は、自然環境のイメージが強いですが「人が手を加えない」という意味ですので、間違った使い方はしていませんよ。
この自然長のばねに質量\(m\)、\(2m\)、\(3m\)のおもりをつけると、おもりの質量に比例して\(x\)、\(2x\)、\(3x\)と、ばねが伸びていきます。
このような関係を見出したのは、フック(\(Hooke\))というイギリスの科学者で、この法則をフックの法則とよびます。
▼\(Hooke\)の法則
\(F=kx\)
\(k[N/m]\):ばね定数
フックの法則の比例定数を、ばね定数といい、ばねのかたさを表しています。
ばね定数が小さいものは、たとえばシャーペンやボールペンの先についているばねのように、指2本でつまんでやれば簡単に形を変えるようなばねです。
ばね定数が大きいものは、車やバスのタイヤのあたりについているサスペンションで、\(5kgf/mm\)のスプリングレートのばねであれば、約\(50000[N/m]\)もの大きさのばね定数ということになります。
工学全般では、ばねが何\(m\)も伸びることはあまり想定しておらず、\(mm\)単位で考えますので、\([N/mm]\)を用いることが多いですが、高校物理では、まずは学問の基礎としてきちんと全体像をマスターするために、他の分野と揃えて\([m]\)単位を使ってばね定数を書き表す慣例があります。
ただ、\([m]\)単位で計算した結果、計算ミスをしても、平然と\(10m\)伸びるばねや、\(100m\)のびるばねを数値で答える人がいます。常識的にあり得ない長さが出てきたら、一度は自分の計算の方を疑ってみてください。
