単振動の特徴

単振動の動きをもう一度ながめてみると、特に数式を追わなくても、次のような特徴には気づけます。
■単振動の物理量の特徴
| 振れ | 変位 | 速さ | 加速度 |
|---|---|---|---|
| 上端 | 最大 | 0 | 最大 |
| 中心 | 0 | 最大 | 0 |
| 下端 | 最大 | 0 | 最大 |
公式を再度確認しておくと、
\(x=Asin\omega t\)
\(v=A\omega cos\omega t\)
\(a=-A\omega^2 sin\omega t\)
の3本でしたので、\(sin\theta\)や\(\cos\theta\)が \(-1\)~\(1\) の間でしか変化しないことを考えると、単純に公式から三角関数を取り払って、正の数としてしまえば、最大値に関してはすぐに求まるということですね。
■最大値の大きさ
| 振れ | 変位 | 速さ | 加速度 |
|---|---|---|---|
| 上端 | \(A\) | 0 | \(A\omega^2\) |
| 中心 | 0 | \(A\omega\) | 0 |
| 下端 | \(A\) | 0 | \(A\omega^2\) |
大きさに関わらず、符号まで考えたいときは、作図して考えてみるといいですね。
仮に、振動中心を原点として、下向きを正とすれば、次のようにまとまります。
■最大値
| 振れ | 変位 | 速さ | 加速度 |
|---|---|---|---|
| 上端 | \(-A\) | 0 | \(A\omega^2\) |
| 中心 | 0 | \(±A\omega\) | 0 |
| 下端 | \(A\) | 0 | \(-A\omega^2\) |
上向きを正とすれば符号が逆になるので、問題文をよく読んで、凡ミスのないようにしましょう。
復元力
加速度に符号までつけて考えると、加速度は常に振動中心の方を向いています。
ということは、その加速度に質量\(m\)をかけ算すると、物理的な意味としては「力」を表すことになり、その力は常に振動中心を向いているということになります。
そんな複雑に考えなくても、単振り子だろうと、バネ振り子だろうと、往復運動をしている物体は、常に中心の方へ戻ろう戻ろうと運動しますよね。
このとき、振動中心に戻ろうとする力のことを「復元力」と言います。
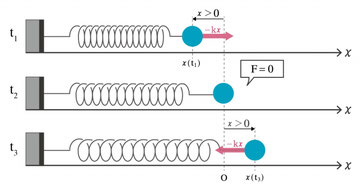
復元力は、振動の中心から離れるほど強い力でかかりますので、中心からの変位\(x\)と比例し、その比例定数を\(K\)とすれば、\(F=-Kx\)という形でかけます。
▼復元力
\(F=-Kx\)
ここで、一般的には\(K\)の中身は何かは分かりませんが、水平ばね振り子の場合は、\(K\)はばね定数\(k[N/m]\)を表すので、イメージしやすいかもしれません。
\(x\)が正のとき、\(F=-Kx\)から、\(F\)は負の値になります。つまり、図のように\(x\)軸の正を設定したとき、物体が\(x\)軸の正の位置にあるときは、力は負の向き、つまり図の左向きを指します。
\(x\)が負のとき、\(F=-K×(-x)\)から、\(F\)は正の値になります。すると力の向きは、図の右向きを指しますので、きちんと復元力が常に振動中心の方を向いているのが確かめられますね。
単振動の運動方程式
単振動の運動方程式は、角振動数\(\omega\)を使って、
\(-m\omega^2 x=-Kx\)
とします。
元々の運動方程式は
\(ma=F\)
ですが、この左辺の加速度に、単振動の加速度\(a=-\omega x^2\)、右辺の力に復元力\(F=-Kx\)を代入した結果、両辺ともにマイナスがつく形となります。
よくある間違いを紹介しておきます。
左辺の加速度にマイナスがつくことを忘れ、右辺の復元力にはマイナスがつくことを覚えている、というタイプの人が結構いるんですね。そうすると、符号バランスは崩れて、
\(m\omega^2 x=-Kx\)
となります。式変形すると、
\(m \omega^2 =-K\)
\(\omega^2=-\displaystyle\frac{K}{m}\)
となり、計算早々に虚数の世界へと旅立たれてしまう人がいます。
単振動で虚数解が出そうなときは、ほとんどの場合で加速度の符号忘れが原因ですので、知っておくといいでしょう。復元力の符号を忘れる人はなぜか少ないんですよ。
▼単振動方程式
\(-m\omega^2 x=-Kx\)
単振動の運動方程式問題の指針
円運動3で書いた説明をもう一度持ってきます。
そもそも運動方程式は何のために解いているのか、それを知らないと、その先にどう解いていけばいいのか迷子になってしまいます。その確認をしておこうと思います。
運動方程式 \(ma=F\) は、本来、加速度を求めるための方程式でした。
加速度を求めて何かいいことがあるのかというと、等加速度3公式に代入すれば、いつ、どの場所に、どのくらいの速度で運動しているかが全て求まるという便利なことがあります。これをしたいから運動方程式を解くわけです。
では単振動方程式ではどうなのか。
単振動方程式は、基本的には、\(ω\) を求める方程式だと思ってくれていいです。
\(ω\) を求めた後は、周期 \(T=\frac{2\pi}{ω}\) の公式に代入すると、結果的に、いつ、どの場所に、どのくらいの速度で運動しているかが全て求まることになります。単振動の場合は、この流れで解きます
▼(復習)周期公式
\(T=\displaystyle\frac{2\pi}{ω}\)
▼運動方程式の解法指針
\(ma=F\) ⇒ \(a\)を求める ⇒ 等加速度3公式に代入
\(-mω^2x=-Kx\) ⇒ \(ω\)を求める ⇒ \(T=\displaystyle\frac{2\pi}{ω}\)に代入
