この講座は、ケプラーの法則が提唱されるに至るまでの前置きの物語です。
物理内容の理解のためであれば、読み飛ばしても、特に問題はありません。
天動説
古代ギリシャが栄える前、地球は平面だと考えられていました。やがて、ギリシャが発展し、前550年ごろにピュタゴラス(ピタゴラス)が現れると、地球は球形だという見方が誕生しました。
大地が平面だと信じられていた時代に、そう解釈するに至った理由は明確ではありませんが、古代エジプトの民がギリシャまで移動すると、ギザのピラミッドとアテネの街とでは緯度にして\(8°\)もの差がありますから、指針としていた天体の観測が肉眼でもわかるレベルで変化することから推測されたと考えられています。
前330年頃のアリストテレスのいた時代まで下ると、船が水平線に消えることからも地球が球形であることが説明されるようになり、前250年頃、エラトステネスの時代には、地学基礎で学習するように、地球が球形であるとしたら、どのくらいの大きさであるのか、という実験がなされ、1周\(46000km\)とほぼ正確に示されるようになりました。
ピタゴラス学派の一派では、地球が宇宙の中心に存在しているから球形であるとしても落ちる先は無く、地球には表裏の概念がない中心地であるとして、物理学的な疑問も解決しています。
ただ、別のピタゴラス一派には、地球が必ずしも中心にあるとは限らず、中心火と呼ばれる仮想天体の周りを回っていると唱えた集団もいました(フィロラオス[BC5c頃])。しかし、空中に浮いている雲はなぜ置いて行かれることがないのか、地球を押すようなものが存在しないのになぜ動き続けていられるのか、といった数々の疑問が投げかけられ、それに対して明確な回答ができず、草創期の地動説を信じる自然哲学者(アリスタルコスなど[BC3c頃])は徐々に数を減らしていきました。
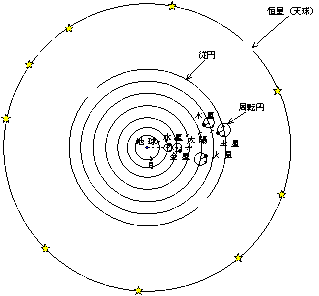
後130年頃、プトレマイオスは、周転円と呼ばれる惑星軌道を考え出しました。地球が宇宙の中心で静止しており、その周囲を様々な天体が周回している。ただし、周回軌道上に周転円と呼ばれる円があり、この円上を運動している、としました。
こうすると、惑星の逆行運動がきれいに説明づくわけです。これによって、わずかに残されていた太陽中心説の一派は完全に駆逐されてしまい、天動説こそが真に正しい理論だとされたわけです。
そののちの時代には、紆余曲折ありますが、地球が宇宙の中心である考え方はキリスト教の考えの助けもあり、長らく信じ続けられていました。
地動説
スペインが1415年に北アフリカのセウタを攻略したあたりの時代から、大航海時代が始まりました。このころになると、天体の観測技術が向上し、天体観測の中での些細な疑問が積み上がっていき、地動説を疑うに至る時代背景が出来上がってきました。
やがて、1543年、日本には鉄砲が伝来する頃、欧州ではコペルニクスが地動説を提唱し、これまでの疑問点を一挙に払拭しました。
雲や鳥が取り残されないのは大気とともに地球が自転していると反論、地球が高速で回っていたら自壊しないか、という問いに対しては、地球が固定されているなら天のすべてのものはもっと高速で動いていると反論、さらに、金星や水星が明け方や宵のすぐにしか観測できない理由も説明し、これまでの矛盾点を次から次へと払拭していきました。
かくして地動説が信じられたかというと、そうではなかったのです。地動説を真とすると、年周視差といわれる現象が見られます。
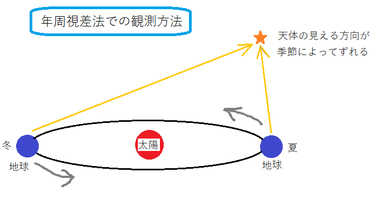
地球が太陽の周囲を交点しているとすると、軌道の反対側から同じ天体を見たときに、幾分かは見え方が変わるはずです。
ところが、この角度が一切観測されない。こうしてコペルニクスの地動説には疑問が残り、万事okとはなりませんでした。
それもそのはずで、最も近い恒星であっても、年周視差は\(0.76\)秒角しかなく、当時の技術で観測するには限界があったのです。
\(0.76\)秒角というのは、三辺が\(271m\)、\(271m\)、\(1mm\)の三角形のとんがりの先くらいの角度ですから、観測は非常に難しいですね。ちなみに最後の3辺目の長さは間違いではありませんよ。1ミリメートルです。
ケプラーの法則
1543年、コペルニクスが地動説を提唱してから、時代が動き始めました。精密な天文観測を行ったデンマークのティコブラーエという天文学者が、ケプラーとともに天文学をまとめ始めます。
ところがティコは、ケプラーの恐るべき能力の高さに気付き、自分の観測結果がすべてケプラーに奪われてしまうと危惧しました。そこで、コペルニクスの地動説を説明するのに、自分が最も使い勝手に困っていた火星の観測データだけをケプラーに渡し、他は自分がすべて抱え込むことにしました。
今でこそ分かっていますが、火星は太陽の周囲を円軌道せず、大幅な楕円軌道を描いていますので、円軌道を前提とした数式処理の中では様々な計算エラーが出てしまうのです。
ところが、ケプラーはそれすらも見抜いてしまい、惑星はそもそも円軌道を描いてはいないと提唱するに至ったのでした。皮肉にもティコが天文学の躍進の後押しをしたわけですね。
その後ケプラーは、「宇宙の神秘」という本で地動説をきちんと提唱してコペルニクスを後押しし、これがのちにガリレイに大きな影響を及ぼしました。このころになると、ティコはケプラーの偉大さは自分とは比較にならないとして、観測結果のすべてをケプラーに託し、1601年に亡くなります。
全ての観測結果を得たケプラーは、続く1609年には「新天文学」という本にケプラー第1、第2法則として知られる理論を提唱、1619年には「世界の調和」という本を出版し、ケプラー第3法則を提唱しました。
そののち、1630年にガリレイが「天文対話」という本で地動説を固めていき、1687年にニュートンが「プリンキピア」を発刊し、自然哲学と宗教の世界から、天文学と物理学が近代科学の論理体系として誕生するに至りました。
ケプラーの時代には、万有引力も物理学も存在していませんでしたので、なぜ天体が何の力を受けることもなく動き続けることができるのか、なぜ完全な円軌道でなく楕円軌道を描くのか、ケプラー自身も納得がいかない気持ち悪さは残していたようです。
そうであっても、そう説明するとすべてきれいに説明ができてしまうから、きっと正しいんだろう、と吹っ切れたあたりは、ケプラーの能力の高さからくるものでしょう。
なぜそうなるか、という哲学的なことではなく、観測結果を式に書き換えるとこう書ける、と物理学的な思考法に移行するのは、高校物理を学んでいる皆さんにも通じるところがあります。
なぜそうなるか、ということのかなりの量が、実は物理学では未知のままなんです。物理はあくまでも、運動の様子を式で表すとどうなるか、という結果ありきの学問なんですね。
