Keplerの第一法則
ケプラーの第一法則(楕円軌道の法則)
それぞれの惑星は、太陽を一つの焦点とする楕円軌道上を運動する。
天体は、円軌道ではなく、楕円軌道を描きます、という経験法則です。楕円に関する理論は、「万有引力1 楕円」にまとめたので、そちらを読んでください。
証明することもできますが、大学の範囲に入りますので、ここでは説明を省略します。極座標表示の運動方程式に、万有引力の式を適用して、動径方向を示してやると、楕円の式そのものが登場します。
なので、ケプラーの第一法則が言っているのは、経験的に楕円っぽい軌道を描いている気がするよ、というわけではなく、厳密に楕円軌道を描きます、ということが数式的に明らかにされている法則です。
Keplerの第二法則
ケプラーの第二法則(面積速度一定の法則)
太陽と惑星とを結ぶ線分が、単位時間に掃く面積は、それぞれの惑星で一定である。
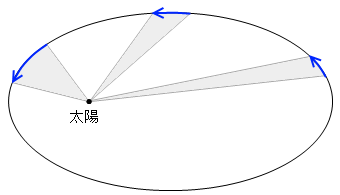
惑星が太陽の周囲を回るとき、太陽に近いところを通過するときは速く通過し、太陽から遠いところを通過するときは遅く通過することが観測結果から知られていました。
この、「速い」「遅い」の程度を厳密に検討してみたところ、一定の時間で進む軌道と、太陽とを扇形状につないでやって面積を出したとき、どの場所でも同じ面積になることが判明しました。
図のようにグレーに色をつけた部分の面積が等しくなるようなイメージですね。
この面積は、単位時間ごとに増えていく量ですので、面積を時間で割った量を、「面積速度」と呼びます。そして、この面積速度が常に一定となるので「面積速度一定の法則」と呼ぶわけです。
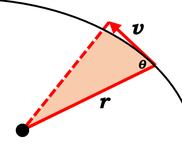
面積速度を式で表してみましょう。軌道上を惑星が、ある速さ\(v\)で進んでいたとします。微小な時間を考えると、惑星が進む距離はごくわずかですので、図の三角形の面積と、扇形の面積は、ほぼ同じものとして考えていいでしょう。
このとき惑星が、わずかな時間\(\Delta t\)で進む距離は、扇形の公式から、\(\Delta x= v \Delta t\)とできます。なので、このときに増える面積(掃く面積)を\(\Delta S\)とすると、
\(\Delta S=\displaystyle\frac{1}{2}r・v\Delta t・sin\theta\)
とできます。この右辺にある微小時間を以降させると、
\(\displaystyle\frac{\Delta S}{\Delta t}=\frac{1}{2}r・v・sin\theta\)
となり、面積速度を求めることができます。これが常に一定であるのが、面積速度一定の法則です。
▼面積速度一定則
\(\displaystyle\frac{1}{2}rvsin\theta=\)一定
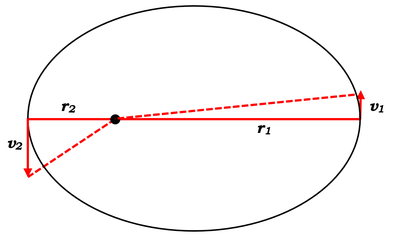
難易度の高くない問題であれば、\(\theta\)がちょうど\(90°\)になる点での問題の頻度の方が出題は多いですので、図のようにして、力のモーメントのつり合いのように
▼面積速度一定則(簡易版)
\(r_1v_1=r_2v_2\)
とした形で、面積速度一定則が登場することが多いかもしれません。
公式ではありませんが、知っておいてもいいかもしれませんね。
Keplerの第三法則
ケプラーの第三法則(調和の法則)
惑星の公転周期\(T\)の2乗は、楕円軌道の半長軸\(a\)の3乗に比例し、その比例定数はすべての惑星で一定となる
惑星軌道がきれいな円であれば円運動の公式を駆使するなどして、比較的簡単に惑星の周期を求めることができますが、楕円軌道をしている惑星の周期を求めようとおもえば、ケプラーの第三法則を使うか、楕円の面積を面積速度で割って求めるか、どちらかの解法をとることになります。
▼調和の法則
\(T^2=ka^3\)
