ホーマン遷移軌道
ホーマン遷移軌道とは、ドイツの\(Walter Hohmann\)(ヴァルター・ホーマン)が\(1925\)年に考え出した、人工衛星の高さ調整のための軌道です。
低軌道を周回している人工衛星の軌道半径を、高い軌道へ移す過程を考えます。このとき、軌道の名前にはいくつかの種類がありますが、今回は気象衛星ひまわりのように、日本の上空で、地球の自転と同じ角速度で回転できるような軌道を狙っていくことにします。このような軌道を「静止軌道」と言い、このような軌道にある人工衛星を「静止衛星」と呼びます。日本の上空で地球の自転と同じ速さで動くのであれば、地上の人間からすれば、まるで静止しているように見えますからね。
ちなみに、静止軌道上の静止衛星は、地球の重力と遠心力がつり合っていなければ存在できませんので、自動的に赤道上空限定になります。気象衛星ひまわりによって撮影される日本の衛星画像は、実は斜め南側から撮影されているものを画像編集で真上から見ているように加工しています。
ホーマン遷移軌道自体は、別に静止軌道を狙わなくても、高い軌道に移れさえすれば何でもホーマン遷移軌道と呼んでいいようです。今回は、静止軌道を狙うホーマン遷移軌道だけ扱いますね。
ホーマン遷移軌道のうち、静止軌道を狙っていく楕円コースのことを特に「静止トランスファ軌道」と呼びます。地球においては、静止衛星の軌道投入では、ほとんどが静止トランスファ軌道を使っています。惑星探査のために使われるような遷移軌道では、二重楕円遷移と言われる、また別の軌道で狙われるので、今回はやめときましょう。
待機軌道上の運動
待機軌道は円軌道なので、円運動の運動方程式の問題として登場します。ほとんどの場合は、速度を聞く問題としてつくられるはずですから、待機軌道での\(v\)を求めてみようと思います。
質量\(m_0\)の人工衛星が、地球の中心から半径\(r\)の軌道上を速度\(v_0\)で周回しているとします。
円運動方程式から、
\(m_0\displaystyle\frac{v_0^2}{r}=G\frac{Mm_0}{r^2}\)
\(v_0^2=\displaystyle\frac{GM}{r}\)
よって
\(v_0=\displaystyle\sqrt{\frac{GM}{r}}\)
宇宙速度の計算のときのように準公式は代入しません。\(GM=gR^2\)の半径\(R\)は地球の半径であって、いま考えている軌道半径\(r\)とは違います。代入したところで何も都合のいいことはおきませんので、ここで終了としておきます。
準公式は、「地表すれすれ」のときに代入しましょう。
待機軌道→遷移軌道
待機軌道から遷移軌道への変換を問う問題は、基本問題では登場しません。基本問題では、「瞬間的に速度を変え」のように、どう変わるかは触れないまま、結果的に速度が○○に変わる、という表現になっていると思います。
この「瞬間的に速度を変え」るときの過程は、ロケット(or燃料)の分離問題ですので、運動量保存則の問題です。そういうわけで、円運動単元では登場せず、入試問題で融合問題として初めて登場するタイプの問題となっていることが多いですね。
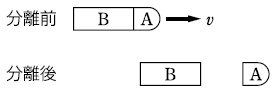
質量\(m_0\)のロケットを分離して、質量\(m\)の頭部\(A\)と、質量\((m_0-m)\)の尾部\(B\)に分かれたとします。\(B\)から見たとき、\(A\)が速さ\(u\)で離れて行くように見えるとき、この2物体の間には
\(v_B+u=v\) \((⇔ v_B=v-u)\)
という関係が成立します。ここで、\(v\)は頭部\(A\)の速度、\(v_B\)は尾部\(B\)の速度です。
運動量保存則から、
\(m_0v_0=mv + (m_0-m)v_B\)
\(m_0v_0=mv + (m_0-m)(v-u)\)
\(m_0v_0=mv + m_0v - m_0u - mv + mu\)
\(m_0v_0=m_0v - (m_0-m)u\)
\(m_0v=m_0v_0+(m_0-m)u\)
\(v=v_0+\displaystyle\frac{m_0-m}{m_0}u\)
つまり、分離後の速度\(v\)を元の2倍にしたければ、\(\displaystyle\frac{m_0-m}{m_0}u=v_0\)、3倍にしたければ、\(\displaystyle\frac{m_0-m}{m_0}u=2v_0\)のように等式を立てて、問題設定に応じて調整してやればいいですね。
遷移軌道上の運動
遷移軌道は楕円軌道なので、円運動方程式は使えません。こういう場合は、力学的エネルギー保存則とケプラー第二法則を利用します。シンプルな問題の場合であれば、このどちらかの法則のみで問題を解くことが出来ますが、しっかりした問題の場合であれば、両方の法則を連立式にして解く問題になります。
また、周期を求める場合はケプラー第三法則を利用します。

仮に、静止軌道が待機軌道の3倍の高さにあったとします。このとき、図の点\(A\)(近地点)での人工衛星の速度を\(v\)、点\(B\)(遠地点)での速度を\(v'\)とします。
■速度に関する問題の解法
点\(A\)と点\(B\)において、力学的エネルギー保存則より、
\(\displaystyle\frac{1}{2}mv^2-G\frac{Mm}{r}=\frac{1}{2}mv'^2-G\frac{Mm}{3r}\)
これだと、\(v\)と\(v'\)がともに未知数なので、式が足りません。そこで、もう一つケプラーの法則から式を持ってきます。
ケプラーの第二法則より
\(\displaystyle\frac{1}{2}rv=\frac{1}{2}・3r・v'\)
ここから式変形して、
\(v=3v' ⇔ v'=\displaystyle\frac{1}{3}v\)
これをエネルギー保存の式に代入すると、
\(\displaystyle\frac{1}{2}mv^2-\frac{GMm}{r}=\frac{1}{2}m\left( \frac{1}{3}v \right) ^2-\frac{GMm}{3r}\)
\(v^2-\displaystyle\frac{2GM}{r}=\frac{1}{9}v^2-\frac{2GM}{3r}\)
\(\displaystyle\frac{8}{9}v^2=\frac{2GM}{r}-\frac{2GM}{3r}\)
\(\displaystyle\frac{8}{9}v^2=\frac{6GM}{3r}-\frac{2GM}{3r}\)
\(\displaystyle\frac{8}{9}v^2=\frac{4GM}{3r}\)
\(v^2=\displaystyle\frac{3GM}{2r}\)
\(v=\displaystyle\sqrt{\frac{3GM}{2r}}\)
よって
\(v’=\displaystyle\frac{1}{3}v=\sqrt{\frac{GM}{6r}}\)
■周期に関する問題の解法
点\(A\)から点\(B\)に達するのに要する時間はどのくらいでしょうか。これを求めるには、楕円軌道の周期\(T\)を求め、その半分の\(\displaystyle\frac{1}{2}T\)を計算すれば求まります。
では、どうやって周期を求めるのか。円軌道の周期は円運動方程式から、楕円軌道の周期はケプラー第三法則から求める、という解法ルールがありました。これに乗っかっていきましょう。
ケプラー第三法則で必要な情報は、軌道の長半径と周期です。待機軌道の長半径は半径そのものですので\(r\)。一方の楕円軌道の長半径は、図より、まず長軸(長い方の直径)が\(r+3r=4r\)であることを求めておいて、その半分の長半径を\(2r\)、とたどっていきます。
待機軌道と遷移軌道における周期の関係は、
\(\displaystyle\frac{r^3}{T_0^2}=\frac{(2r)^3}{T^2}\)
\(\displaystyle\frac{1}{T_0^2}=\frac{8}{T^2}\)
\(T^2=8T_0^2\)
\(T=2\sqrt{2}T_0\)
ここで、待機軌道の周期\(T_0\)を求めておきます。待機軌道での速度
\(v_0=\displaystyle\sqrt{\frac{GM}{r}}\)
までは求まっているので、
\(T_0=\displaystyle\frac{2\pi r}{v_0}\) より
\(T_0=2\pi r ・\displaystyle\sqrt\frac{r}{GM}\)
\(T_0=2\pi ・\displaystyle\sqrt\frac{r^3}{GM}\)
よって
\(T=2\sqrt{2}T_0=4\pi \displaystyle\sqrt\frac{2r^3}{GM}\)
\(\displaystyle\frac{1}{2}T=2\pi \displaystyle\sqrt\frac{2r^3}{GM}\)
これが軌道の遷移に要する時間です。
遷移軌道→静止軌道
再び運動量保存則の問題。です。待機軌道から遷移軌道に移る過程と同じですが、この高さまで上がると、完全に宇宙空間ですから、もはやロケットを切り離していくような高さではありませんので、燃料を噴射して速度を上げる設定にされると思います。
気体の燃料には形がありませんので、立式に戸惑う人もいるかもしれません。ですが、運動量保存則における質量は、物体の形状とは関係がありませんので、トータルでどのくらいの質量の燃料を放出したかさえわかれば計算が可能です。
まして、放出された燃料がどのくらいの速度で移動するのかは今あまり興味がないことで、人工衛星の方がどのくらいの速度になるかを求める問題となるはずです。なので、待機軌道から遷移軌道に移る過程の考え方と同じになります。
静止軌道上の運動
静止軌道と名前がついているものの、これも円運動ですから、円運動の運動方程式の問題です。
待機軌道で速度を求めた結果が
\(v_0=\displaystyle\sqrt{\frac{GM}{r}}\)
でしたので、この式における\(r\)を\(3r\)に置換してやれば、
\(V=\displaystyle\sqrt{\frac{GM}{3r}}\)
と、すぐに求めることができますね。
また、周期に関しても、待機軌道で求めた周期
\(T_0=2\pi ・\displaystyle\sqrt\frac{r^3}{GM}\)
において、同じく\(r\)を\(3r\)に置換してやれば、
\(T’=2\pi ・\displaystyle\sqrt\frac{(3r)^3}{GM}\)
とするだけで求まります。
さて、静止軌道の場合、とても重要な設定があります。それは地球自転との関係性の問題です。
静止衛星が地表に対して静止するためには、静止衛星の周期が地球の周期と等しくならなければいけませんね。
これを利用して、静止衛星の軌道半径\(3r\)の部分が、実際にはどのくらいの高度になるのか、数値計算をしてみましょう。
\(T’=T_{地}=2\pi ・\displaystyle\sqrt\frac{(3r)^3}{GM}\) より
\(3r=\displaystyle\sqrt[ 3 ]{\frac{GMT_{地}^2}{4\pi ^2}}\)
\(G=6.7×10^{-11}N・m^2/kg^2\)、\(M=6.0×10^{24}kg\)、\(T_{地}=86400s\)を代入すると、
\(3r≒4.2×10^7m=4.2×10^4km\)
地球の中心から、だいたい\(42000km\)の軌道ですので、地球の半径が約\(6000km\)として、高度\(36000km\)くらいの軌道が静止衛星の軌道になります。
これよりも高くても低くても静止を保つことはできませんので、赤道上空\(36000km\)付近の軌道上には各国の衛星がたくさんひしめいています。
万有引力分野がついに終わりました。
これにて力学分野は終了です。


