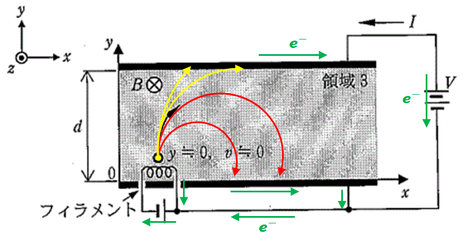
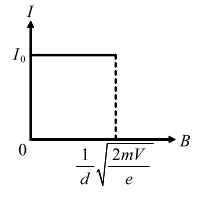
■解答
(イ) \(\displaystyle\frac{l}{v_0}\) (ロ) \(\displaystyle\frac{1}{2}･\frac{eV}{md}･\frac{l^2}{v_0^2}\) (ハ) \(\displaystyle\sqrt{v_0^2+(\frac{eVl}{mdv_0})^2}\)
(ニ) \(\displaystyle\frac{eVl(l+2L)}{2mdv_0^2}\) (ホ) \(\displaystyle\frac{Vl(l+2L)}{4dV_p}\) (ヘ) \(\displaystyle\sqrt{\frac{2eVy}{md}}\)
(ト) \(\displaystyle\frac{2mV}{eB^2d}\) (チ) \(-\displaystyle\frac{eV}{md}\) (リ) ①\(x\)軸の正 (ヌ) ①\(y_U<d-y_w\)
■解説
(イ)
電子は\(x\)軸方向には等速運動をしているので、
\(t=\displaystyle\frac{l}{v_0}\)
(ロ)
\(y\)軸方向の運動方程式より
\(ma=eE\)
\(ma=e\displaystyle\frac{V}{d}\)
\(a=\displaystyle\frac{eV}{md}\)
であるから、等加速度運動の公式に代入して
\(y=\displaystyle\frac{1}{2}at^2\)
\(=\displaystyle\frac{1}{2}･\frac{eV}{md}･\frac{l^2}{v_0^2}\)
(ハ)
点\(P\)での速度の\(y\)成分は、
\(v_{Py}=at\)
\(=\displaystyle\frac{eVl}{mdv_0}\)
であり、\(x\)成分は\(v_{Px}=v_0\)であるから、
\(v=\sqrt{v_{Px}^2+v_{Py}^2}\)
\(=\sqrt{v_0^2+(\displaystyle\frac{eVl}{mdv_0})^2}\)
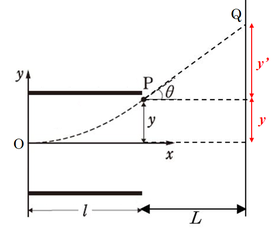
(ニ)
図のように\(y'\)をおくと、点\(P\)での速度成分より
\(L:y'=v_0:at\)
と書けるので、
\(v_0y'=Lat\)
\(y'=\displaystyle\frac{L}{v_0}･\frac{eVl}{mdv_0}\)
\(=\displaystyle\frac{LeVl}{mdv_0^2}\)
ゆえに
\(y+y'=\displaystyle\frac{eVl^2}{2mdv_0^2}+\frac{Levl}{mdv_0^2}\)
\(=\displaystyle\frac{eVl(l+2L)}{2mdv_0^2}\)
(ホ)
「電子が領域１に侵入する前に、あらかじめ電圧\(V_P(>0)\)で速さ\(0\)から\(v_0\)まで加速され」とあるので、エネルギー保存則より、
\(eV_P=\displaystyle\frac{1}{2}mv_0^2\)
\(v_0^2=\displaystyle\frac{2eV_P}{m}\)
であるから、
\(y+y'=\displaystyle\frac{eVl(l+2L)}{2mdv_0^2}\)
\(=\displaystyle\frac{eVl(l+2L)}{2md}･\frac{m}{2eV_P}\)
\(=\displaystyle\frac{Vl(l+2L)}{4dv_P}\)
(へ)
ローレンツ力は仕事をしないので、電場がした仕事から
\(W=K\)
\(e\displaystyle\frac{V}{d}×y=\frac{1}{2}mv^2\)
\(v=\displaystyle\sqrt{\frac{2eVy}{md}}\)
(ト)
点\(U\)における速度が
\(v=v_x=\displaystyle\frac{2V}{Bd}\)
であるから
\(\displaystyle\frac{2V}{Bd}=\sqrt{\frac{2eVy_U}{md}}\)
\(\displaystyle\frac{4V^2}{B^2d^2}=\frac{2eVy_U}{md}\)
\(y_U=\displaystyle\frac{4V^2}{B^2d^2}･\frac{md}{2eV}\)
\(=\displaystyle\frac{2mV}{eB^2d}\)
(チ)
点\(U\)における運動方程式より
\(ma=eE-evB\)
\(=e\displaystyle\frac{V}{d}-e\frac{2V}{Bd}B\)
\(-\displaystyle\frac{eV}{d}\)
\(a=-\displaystyle\frac{eV}{md}\)
(リ)
電子の運動が時計回りなので、陽イオンの運動は反時計回りだと判断できる。
よって、①\(x\)軸の正 の向きに移動する。
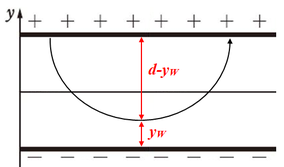
(ヌ)
(ト)より、電子の円軌道半径と陽イオンの円軌道半径はそれぞれ、
\(y_U=\displaystyle\frac{2mV}{eB^2d}\)
\(d-y_W=\displaystyle\frac{2MV}{eB^2d}\)
いま、\(M>m\)が成り立つので
\(d-y_W=\displaystyle\frac{2MV}{eB^2d}>\frac{2mV}{eB^2d}=y_U\)
よって \(y_U<d-y_W\) ①
(3)
\(y_U=\displaystyle\frac{2mV}{eB^2d}>d\) のとき、回路に\(I_0\)が流れる。
\(y_U<d\) のとき、電子は－極板に戻り、回収される
\(y_U=d\) のとき、つまり
\(\displaystyle\frac{2mV}{eB^2d}=d\)
\(B=\displaystyle\sqrt{\frac{2mV}{ed^2}}=\frac{1}{d}\sqrt{\frac{2mV}{e}}\)
のときが回路に電流が流れるための最大の\(B\)となるので、\(I-B\)グラフは次のようになる。
