■解答
問１ \(V_1=\displaystyle\frac{C_1}{C_1+C_2}E\) 問２ \(V_2=\displaystyle\frac{C_1C_2}{(C_1+C_2)(C_2+C_3)}E\) 問３ \(V_3=\displaystyle\frac{C_1}{C_1+C_2+C_3}E\)
問４ \(\varepsilon_r=\displaystyle\frac{C_1-2C_2}{2C_3}\) 問５ \(I_0=E\displaystyle\sqrt{\frac{C}{L}}\) 問６ \(H_0=nI_0\)
問７ \(t_0=\displaystyle\frac{\pi}{2}\sqrt{LC}\) 問８ \(\displaystyle\frac{\Delta I}{I_0\Delta t}=-\frac{R}{L}\)
問９\((t≦t_0)\) (あ) \((t>t_0)\) (か)
■解説
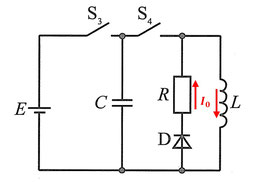
問１
回路全体の合成容量は
\(C_全\displaystyle\frac{C_1C_2}{C_1+C_2}\)
なので、コンデンサー１，２に蓄えられた電気量は、どちらも
\(Q=\displaystyle\frac{C_1C_2}{C_1+C_2}E\)
となります。また、コンデンサー２の極板間の電位差を\(V_1\)とすると、
\(Q=C_2V_1\)
とも表せますから、この両者をつないで、
\(C_2V_1=\displaystyle\frac{C_1C_2}{C_1+C_2}E\)
\(V_1=\displaystyle\frac{C_1}{C_1+C_2}E\)
問２
スイッチ\(S_1\)を閉じると、コンデンサー\(C_1\)と\(C_2\)が充電されます。\(C_3\)の電気量はゼロのままです。
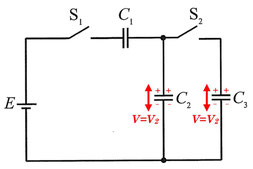
その後、スイッチ\(S_1\)を開いてからスイッチ\(S_2\)を閉じると、コンデンサー\(C_2\)が放電され\(C_3\)が充電されます。\(C_1\)の電荷は図の左側の極板に蓄えられている電荷の移動先がないため放電されず、フル充電されたままですので、問題を解く上では右側の閉回路だけを考えればいいことになります。(図はスイッチ\(S_2\)を閉じるのを描き忘れています)
電気量保存則より、
\(C_2V_1=C_2V_2+C_3V_2\)
\(\displaystyle\frac{C_1C_2}{C_1+C_2}E=(C_2+C_3)V_2\)
\(V_2=\displaystyle\frac{C_1C_2}{(C_1+C_2)(C_2+C_3)}E\)
問３
図の赤で示した部分は、回路から孤立しています。この部分の電気量の総和はゼロになっていることに着目して、電気量保存則を利用しましょう。(図はコンデンサー\(C_1\)に蓄えられている電荷の符号が逆です。ここの符号が重要なので気をつけてください)
\(C_1\)に負、\(C_2\)と\(C_3\)に正の電荷が帯電していますので、電気量保存則より、
\(0=-C_1(E-V_3)+C_2V_3+C_3V_3\)
\(=-C_1E+C_1V_3+C_2V_3+C_3V_3\)
\(C_1E=(C_1+C_2+C_3)V_3\)
\(V_3=\displaystyle\frac{C_1}{C_1+C_2+C_3}E\)
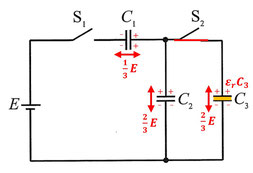
問４
コンデンサー２の電位差がコンデンサー１の電位差の２倍になっていて、コンデンサー２とコンデンサー３は並列接続のため電位差が等しくなります。
なので、各コンデンサーの電位差は図のようになります(こちらの図も\(C_1\)に蓄えられている電荷の符号が逆なので気をつけてください)
この問題は主には２パターンの解き方が思いつきます。
一つは前問と同じように電気量保存則で力押ししてしまうパターン。もう一つは問３の結果から、物理量の一部を置換して考える解き方です。
両方やってみましょう。
■電気量保存則で解く
問３と同様、孤立部分の電気量の総和がゼロなので、
\(0=-\displaystyle\frac{1}{3}C_1E+\frac{2}{3}C_2E+\frac{2}{3}\varepsilon_rC_2E\)
\(=-C_1+2C_2+2\varepsilon_rC_3\)
\(2\varepsilon_rC_3=C_1-2C_2\)
\(\varepsilon_r =\displaystyle\frac{C_1-2C_2}{2C_3}\)
■置換して解く
問３の\(V_3\)において、\(V_3\rightarrow V'_3=\displaystyle\frac{2}{3}E\)、\(C_3\rightarrow \varepsilon_rC_3\) と置換して、
\(V_3=\displaystyle\frac{C_1}{C_1+C_2+C_3}E\)
\(\rightarrow\)
\(\displaystyle\frac{2}{3}E=\frac{C_1}{C_1+C_2+\varepsilon_rC_3}E\)
\(\displaystyle\frac{3}{2}=\frac{C_1+C_2+\varepsilon_rC_3}{C_1}\)
\(\displaystyle\frac{3C_1}{2}=C_1+C_2+\varepsilon_r C_3\)
\(\varepsilon_rC_3=\displaystyle\frac{3C_1}{2}-C_1-C_2\)
\(=\displaystyle\frac{C_1-2C_2}{2}\)
\(\varepsilon_r=\displaystyle\frac{C_1-2C_2}{2C_3}\)
問５
\(S_4\)を閉じたあと、コイルに流れる電流が増加している間、ダイオードがあるため抵抗には上から下には電流が流れません。
この間のエネルギー保存則より、
\(\displaystyle\frac{1}{2}CE^2=\frac{1}{2}LI_0^2\)
\(I_0=E\sqrt{\displaystyle\frac{C}{L}}\)
問６
ソレノイドコイルの内部の磁場の大きさは
\(H=nI\)
で表され、電流の大きさのみで決まります。よって、コイルに流れる電流の大きさが最大値\(I_0\)となるとき、磁場の大きさが最大となるので、
\(H_0=nI_0\)
となります。
問７
磁場の大きさが最大になるまでの間は、\(LC\)振動回路とみなすことができます。
その時間は\(\displaystyle\frac{T}{4}\)に相当しますので、
\(t_0=\displaystyle\frac{T}{4}\)
\(=\displaystyle\frac{1}{4}･2\pi \sqrt{LC}\)
\(=\displaystyle\frac{\pi}{2}\sqrt{LC}\)
問８
スイッチを開いた瞬間、\(I=I_0\)でダイオードと抵抗に電流が流れます。
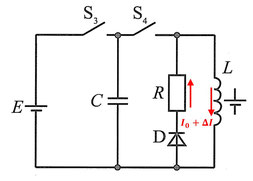
その後、時刻\(t_0\)の微小時間\(\Delta t\)後には、\(I=I_0+\Delta I\)となり。コイルに誘導起電力が生じます。
このとき、キルヒホッフ第二法則により、
\(-L\displaystyle\frac{\Delta I}{\Delta t}=R(I_0+\Delta I)\)
\(-L\displaystyle\frac{\Delta I}{\Delta t}=RI_0+R\Delta I\)
\(-L\Delta I=RI_0\Delta t+R\Delta I\Delta t\)
この右辺第二項はデルタ量とデルタ量の積で十分小さいので、微小量として落としてしまいます。
仮に数値を入れたとしても有効数字のずっと下のケタになると思います。
\(-L\Delta I≒RI_0\Delta t\)
よって
\(\displaystyle\frac{\Delta I}{I_0\Delta t}=-\frac{R}{L}\)
問９
\(0≦t≦t_0\)のとき
回路は\(LC\)振動回路と見なせますので、電流の大きさは\(\sin\)カーブを描きます。 ⇒(あ)
\(t_0≦t\)のとき
問８より
\(\displaystyle\frac{\Delta I}{\Delta t}=-\frac{R}{L}I_0\)
が成り立つので、時間とともに\(I\)は減少していきます。また、そのときの減少率自体も時間とともに小さくなっていきます。 ⇒(か)
問９(別)
一応、計算して求めることもできます。
問８から、
\(\displaystyle\frac{dI}{I dt}=-\frac{R}{L}\)
\(\displaystyle\int\frac{dI}{I}=^\frac{R}{L}\int dt\)
\(\log|I|=-\displaystyle\frac{R}{L}t+C\) (\(C\)は積分定数)
\(t=t_0\)のとき、\(I=I_0(>0)\)なので、
\(\log I_0=-\displaystyle\frac{R}{L}t_0+C\)
よって
\(C=\log I_0+\displaystyle\frac{R}{L}t_0\)
ゆえに
\(\log I=-\displaystyle\frac{R}{L}t+\log I_0 +\frac{R}{L}t_0\)
\(\log\displaystyle\frac{I}{I_0}=-\frac{R}{L}(t-t_0)\)
\(\displaystyle\frac{I}{I_0}=\exp\left(-\displaystyle\frac{R}{L}(t-t_0)\right)\)
\(I=I_0\exp\left(-\displaystyle\frac{R}{L}(t-t_0)\right)\)
⇒(か)
となりますが、計算で求める人はほぼいないと思います。
