■解答
問1 \(\displaystyle\frac{3}{2}nR\Delta T\) 問2 \(\displaystyle\sqrt{\frac{nRT}{k}}\)
問3 \(\Delta Q=2nR\Delta T\) \(C=2nR\) 問4 \( \displaystyle\frac{F}{2k}+\sqrt{\left( \displaystyle\frac{F}{2k} \right)^2+\frac{nRT}{k}}\)
問5 グラフ:略 式:\(\displaystyle\frac{1}{2}\left(\frac{F}{F_0}\right) + \sqrt{\frac{1}{4}\left(\frac{F}{F_0}\right)^2+1}\)
問6(a) \(1\) (b) \(2\)
■解説
問1
\(\Delta U =\displaystyle\frac{3}{2}nR\Delta T\) となるから、
熱力学第一法則より、
\(\Delta Q= \Delta U\)
\(=\displaystyle\frac{3}{2}nR\Delta T\)
問2
\(PV=nRT\) より
\(PSx=nRT\)
\(PS=\displaystyle\frac{nRT}{x}\)
よって力のつり合いから
\(PS=kx\) なので、
\(\displaystyle\frac{nRT}{x}=kx\)
\(x^2=\displaystyle\frac{nRT}{k}\)
\(x=\displaystyle\sqrt{\frac{nRT}{k}}\)
問3
\(\Delta U =\displaystyle\frac{3}{2}nR\Delta T\) となるから、
熱力学第一法則より
\(\Delta Q = \Delta U +W\)
ここで、\(W\)は、ばねが蓄えた弾性エネルギーに相当するので、\(W=\displaystyle\frac{1}{2}k(\Delta x)^2\)
よって
\(\Delta Q=\displaystyle\frac{3}{2}nR\Delta T +\displaystyle\frac{1}{2}k(\Delta x)^2\)
\(\Delta x= \sqrt{\displaystyle\frac{nR\Delta T}{k}}\)なので、
\(\Delta Q=\displaystyle\frac{3}{2}nR\Delta T+\frac{1}{2}k・\displaystyle\frac{nR\Delta T}{k}\)
\(=\displaystyle\frac{3}{2}nR\Delta T+ \frac{1}{2}nR\Delta T\)
\(=2nR\Delta T\)
また、系全体の熱容量を\(C\)とすると、
\(\Delta Q=C\Delta T\)
\(2nR\Delta T=C\Delta T\)
\(C=2nR\)
問4 問2と同様に計算して、
\(PS=\displaystyle\frac{nRT}{x}\)
よって、力のつりあいの式は
\(\displaystyle\frac{nRT}{x}+F=kx\)
\(nRT+Fx=kx^2\)
\(0=kx^2-Fx-nRT\)
よって
\(x=\displaystyle\frac{F+\sqrt{F^2 +4knRT}}{2k}\)
問5
\(F=0\)のとき、
\(x_0=\displaystyle\frac{\sqrt{4knRT}}{2k}\)
\(=\sqrt{\displaystyle\frac{nRT}{k}}\)
\(nRT=kx_0^2\)
ここに、\(F_0=kx_0\)を適用すると、
\(nRT=F_0x_0\)
であるから、問4の式に代入すると、
\(x=\displaystyle\frac{1}{2}・\frac{x_0}{F_0}\left( F+\sqrt{F^2+4\frac{F_0}{x_0}・F_0x_0} \right)\) (∵\(k=\frac{F_0}{x_0}\)、\(nRT=F_0x_0\)
\(=\displaystyle\frac{x_0}{2F_0} \left( F+\sqrt{F^2 +4F_0^2} \right) \)
\(\displaystyle\frac{x}{x_0}=\frac{1}{2} \left[ \frac{F}{F_0}+\sqrt{\left(\frac{F}{F_0}\right)^2 +4}\right]\)
となる。
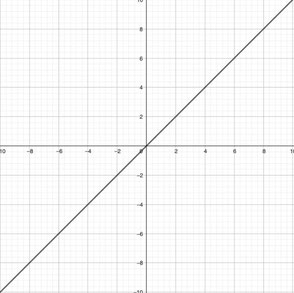
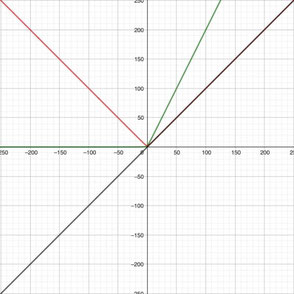
これを、\(y=x+\sqrt{x^2+4}\)として見たとき、
第一項の\(y=x\)の部分が
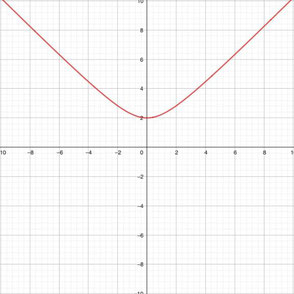
第二項の\(y=\sqrt{x^2+4}\)の部分が
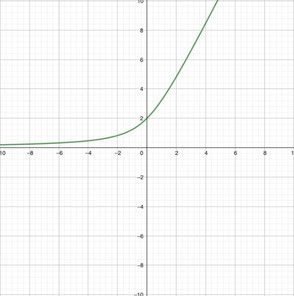
なので、合算したときの解答(問5の解答)は次の図のとおり。
縦軸は\(\displaystyle\frac{x}{x_0}\)
横軸は\(\displaystyle\frac{F}{F_0}\)
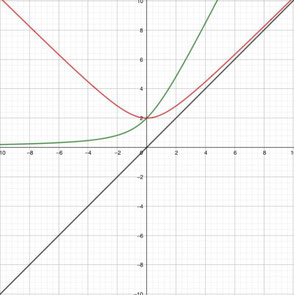
これらを重ねて図示してみると、次のようになる。
このとき、第二項のグラフは双曲線を描いているので、軸の幅をグッと遠ざけて見てみると、次のように図示できるので、納得できるのではないでしょうか。
問6
\(\displaystyle\frac{x}{x_0}=\frac{1}{2}\left[ \displaystyle\frac{F}{F_0}+\sqrt{\left(\frac{F}{F_0} \right)^2 +4}\right]\) ―(*)
\(\displaystyle\frac{x+\Delta x}{x_0}=\frac{1}{2}\left[ \frac{F+\Delta F}{F_0}+\sqrt{\left(\frac{F+\Delta F}{F_0}\right)^2+4}\right]\) ―(**)
(a)
\(\displaystyle\frac{F}{F_0}\)が限りなく大きいとき、
(*)式は、
\(\displaystyle\frac{x}{x_0}=\displaystyle\frac{1}{2}\left( \frac{F}{F_0}+\frac{F}{F_0} \right)\)
\(\displaystyle\frac{x}{x_0}=\displaystyle\frac{F}{F_0}\)
(**)式は、
\(\displaystyle\frac{x+\Delta x}{x_0}=\displaystyle\frac{1}{2}\left( \frac{F+\Delta F}{F_0}+\frac{F+\Delta F}{F_0} \right)\)
\(\displaystyle\frac{x+\Delta x}{x_0}=\displaystyle\frac{F+\Delta F}{F_0}\)
よって、
\(\displaystyle\frac{\Delta x}{x_0}=\displaystyle\frac{\Delta F}{F_0}\)
\(\displaystyle\frac{F_0}{x_0}=\displaystyle\frac{\Delta F}{\Delta x}\)
\(k=k_{eff}\)
ゆえに、
\(\displaystyle\frac{k_{eff}}{k}=1\)
(b)
\(\displaystyle\frac{F}{F_0}=0\)のとき、
(**)式は、
\(\displaystyle\frac{x+\Delta x}{x_0}=\displaystyle\frac{1}{2}\left[ \frac{\Delta F}{F_0}+\sqrt{\left(\frac{\Delta F}{F_0}\right)^2+4 }\right]\)
(*)式より
\(\displaystyle\frac{x}{x_0}=\frac{1}{2}\sqrt{4}=1\)
なので、
\(1+\displaystyle\frac{\Delta x}{x_0}=\displaystyle\frac{\Delta F}{2F_0}+\frac{1}{2}\sqrt{\left(\frac{\Delta F}{F_0}\right)^2+4}\)
2次の項は無視できるので、この式のルートの中の\(2\)乗がつく項は十分小さいとしてゼロに近似してしまいましょう。すると
\(1+\displaystyle\frac{\Delta x}{x_0}=\displaystyle\frac{\Delta F}{2F_0}+1\)
ゆえに、
\(2\displaystyle\frac{F_0}{x_0}=\frac{\Delta F}{\Delta x}\)
\(2k=k_{eff}\)
\(\displaystyle\frac{k_{eff}}{k}=2\)
問7
引力が\(F=kr\)で表せることから、\(AB\)間は、ばねでつながっていると見立てることができる。
(a) ばねの弾性力による位置エネルギーと見立てて、
\(U=\displaystyle\frac{1}{2}kr^2\)
(b) \(\displaystyle\frac{Mv^2}{r}=kr\)
(c) (b)より
\(Mv^2=kr^2\)
\(\displaystyle\frac{1}{2}Mv^2=\frac{1}{2}kr^2\)
であるから、
\(E=K+U\)
\(=\displaystyle\frac{1}{2}kr^2+\frac{1}{2}kr^2\)
\(=kr^2\)
(d) 物質波(ド・ブロイ波)の波長は、運動量の逆数に比例し、
\(\lambda_B=\displaystyle\frac{h}{Mv}\)
と書ける。(b)より、
\(Mv^2=kr^2\)
\(v=r\sqrt{\displaystyle\frac{k}{M}}\)
であるから、
\(\lambda_B=\displaystyle\frac{h}{M}・\frac{1}{r}\sqrt{\frac{M}{k}}\)
\(=\displaystyle\frac{h}{r\sqrt{kM}}\)
(e) ボーアの量子条件は、
\(2\pi r_n=n\lambda_B\)
\(2\pi r_n=n・\displaystyle\frac{h}{r_n\sqrt{kM}}\)
\(r_n^2=\displaystyle\frac{nh}{2\pi \sqrt{kM}}\)
\(r_n=\displaystyle\sqrt{\frac{nh}{2\pi \sqrt{kM}}}\) \((n=1,2,3,…)\)
(f) \(E=kr^2\) より
\(E_n=kr_n^2\)
\(=\displaystyle\frac{nhk}{2\pi\sqrt{kM}}\)
\(=\displaystyle\frac{nh}{2\pi}\sqrt{\frac{k}{M}}\) \((n=1,2,3,…)\)
(g) ボーアの振動数条件は、
\(\Delta E_{ln}=E_l-E_n\)
\(=(l-n)・\displaystyle\frac{h}{2\pi}\sqrt{\frac{k}{M}}\)
(h) \(\Delta E_{ln}=h\nu\) より
\(\nu=\displaystyle\frac{\Delta E_{ln}}{h}\)
また、\(c=\nu \lambda_{ln}\) より
\(c=\displaystyle\frac{\Delta E_{ln}}{h}・\lambda_{ln}\)
\(\lambda_{ln}=\displaystyle\frac{hc}{\Delta E_{ln}}\)
\(=hc・\displaystyle\frac{2\pi}{(l-n)h}\sqrt{\frac{M}{k}}\)
\(=\displaystyle\frac{2\pi c}{l-n}\sqrt{\frac{M}{k}}\)