静電エネルギー
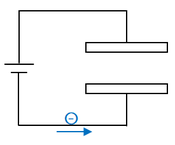
コンデンサーを充電する過程を、電子一つずつのレベルで考えてみます。
まず最初に、極板に電荷が蓄えられておらず、極板間に電圧がかかっていない状態で、電子を一つ送り込みます。このときに電池がした仕事は、
\(W=qV\)
で計算ができますが、\(V=0\)なので、
\(W=0\)
です。
「仕事=力×距離」の観点から見れば、極板に電荷がないので、力なしで電荷を送り込むことができる、ということになります。

少し充電されたあとに、さらに電荷を送り込もうとすると、極板に電荷が少し蓄えられているので、極板にいる電荷と、送り込む電荷との間に反発力がはたらきます。
極板に蓄えられた電気量が増えれば増えるほど、反発力が強くなるので、電荷を一つ充電するだけで大きな仕事が必要になります。
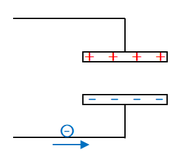
少し充電されたあとに、さらに電荷を送り込もうとすると、極板に電荷が少し蓄えられているので、極板にいる電荷と、送り込む電荷との間に反発力がはたらきます。
極板に蓄えられた電気量が増えれば増えるほど、反発力が強くなるので、電荷を一つ充電するだけで大きな仕事が必要になります。
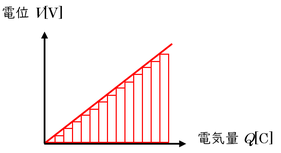
縦軸を電位、横軸を電気量にして、この充電過程をグラフ化してみました。
一つ目の電子を充電させるときは、\(W_1=qV_1=0[J]\)、二つ目の電子を充電させるときは少し高くなった\(V\)を使って、\(W_2=qV_2\)、三つ目の電子を充電するときは、さらに極板間の電位差が\(V\)だけ高くなって\(W_3=qV_3\)…となり、充電するのに電池がした仕事の総量は、グラフの三角形の面積を計算すればいいことになります。
▼静電エネルギー
\(U=\displaystyle\frac{1}{2}QV\)
\(U=\displaystyle\frac{1}{2}CV^2\)
\(U=\displaystyle\frac{Q^2}{2C}\)
