■解答
問１ \(\alpha=\displaystyle\frac{2\pi f_1L}{V}\) 問２ \(\displaystyle\frac{L}{V}\) 問３ \(\beta=\displaystyle\frac{2\pi f_2L}{V}\)
問４ \(t_2=\displaystyle\frac{V-u}{V}t_1+\frac{L}{V}\) 問５ \(f_2=\displaystyle\frac{V}{V-u}f_1\) 問６ \(2A_2\sin(2\pi f_1t-\alpha)\)
問７ \(x=\displaystyle\frac{V}{4f_1}\)
■解説
問１
音源の所での波形が
\(A_1\sin(2\pi f_1t)\)
で表される、とありますので、これを使いましょう。音源から音が出て、マイクのところに伝わるのに少しの時間がかかります。
その時間の遅れを修正すると、マイクのところでの音の波形を表す式は
\(A_2\sin[2\pi f_1(t-t_0)]\)
となります。音の振幅は、音波に減衰や重ね合わせがなければ\(A_1\)のままですが、一般的には値が変わります。それを問題文では\(A_2\)と設定していますので、それを使います。
時間の遅れは、音が距離\(L\)を速さ\(V\)で進む時間ですので、
\(t_0=\displaystyle\frac{L}{V}\)
となり、
\(A_2\sin\left[2\pi f_1\left(t-\displaystyle\frac{L}{V}\right)\right]\)
\(A_2\sin \left(2\pi f_1t-2\pi f_1 \displaystyle\frac{L}{V}\right)\)
よって、
\(\alpha=\displaystyle\frac{2\pi f_2 L}{V}\)
問２
音源が動いていても静止していても、一度空気中に発せられてしまった音の振動は、変わらず進みます。
音が距離\(L\)を速さ\(V\)で進む時間は、問１と同じく
\(t'_0=\displaystyle\frac{L}{V}\)
となります。
問３
音源が動いていても、音速は変わりません。なので、時刻\(t=0\)に音源が\(x=-L\)にあり、ここから出た音は、振動数の違いこそあれ、問１と状況は同じです。音源からマイクに伝わる間に、\(t'_0=\displaystyle\frac{L}{V}\) だけ遅れが生じ、
\(A_2\sin \left(2\pi f_2t- 2\pi f_2 \displaystyle\frac{L}{V}\right)\)
の波形がマイクのところで観測されますので、
\(\beta=\displaystyle\frac{2\pi f_2 L}{V}\)
問４
\(t=t_1\)には、音源は少し進んでいます。音源の速さが\(u\)ですので、\(ut_1\)だけ進んでいることになりますね。
すると、この瞬間には音源からマイクまでの距離は\(L-ut_1\)になっていますので、このとき発せられた音がマイクに到達するまでの時間は、
\(\displaystyle\frac{L-ut_1}{V}\)
となります。
ところで、時間のカウントのしかたは、音源がはじめ\(-L\)にいたときを起点としていますので、\(t_1\)だけ経過してから、\(\displaystyle\frac{L-ut_1}{V}\)の伝播があることになります。よって、
\(t_1+\displaystyle\frac{L-ut_1}{V}\)
\(=\displaystyle\frac{V}{V}t_1+\frac{L}{V}-\frac{ut_1}{V}\)
\(=\displaystyle\frac{L}{V}+\frac{V-u}{V}t_1\)
問５
音源が\(t=t_1\)に発している音は、振動数\(f_1\)です。
一方、マイクが受け取る音は、ドップラー効果が起こる都合上、振動数が\(f_2\)となり、受け取るときの時間は\(t=t_2\)。
さらに、音源からマイクに音が伝わる時間的な遅れのために、位相が\(\beta\)だけズレることになりますので、その差の修正もしてやると、位相が等しくなるには
\(2\pi f_1t_1=2\pi f_2t_2-\beta\)
となります。
ですが、問題を解くだけならここに理論的な理解はあまりいらず、リード文から「音源の所での波形は\(A_1\sin(2\pi f_1t)\)で表される」を読み、問３から「マイクロホンで測定した波形は\(A_2\sin(2\pi f_2t-\beta)\)であった」を読めれば、その位相の部分だけを比べるようにと指示が出ている問５では、なかば自動的に \(2\pi f_1t_1=2\pi f_2t_2-\beta\) と立式することになるかと思います。振幅は比較しませんので置いときます。
よって、
\(2\pi f_1t_1=2\pi f_2t_2-\beta\)
\(2\pi f_1t_1=2\pi f_2\left(\displaystyle\frac{L}{V}+\frac{V-u}{V}t_1\right)-\displaystyle\frac{2\pi f_2 L}{V}\)
\(f_1t_1=f_2\left(\displaystyle\frac{L}{V}+\frac{V-u}{V}t_1\right)-\displaystyle\frac{f_2 L}{V}\)
\(f_1t_1=f_2\left(\displaystyle\frac{V-u}{V}t_1\right)\)
\(f_1=\displaystyle\frac{V-u}{V}f_2\)
もしくは、
\(f_2=\displaystyle\frac{V}{V-u}f_1\)
問６
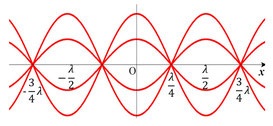
両方の音源から同時に音が発せられると、この間には定常波ができます。
音源から音源までの線分上には音が大きくなっている「腹」と音が打ち消される「節」が交互に並んでいるはずですが、その中点にマイクがあれば、少なくともそこは「腹」になっていることがわかります。
腹では振幅が２倍になり、その他は変化しませんので、
\(2A_2\sin(2\pi f_1t-\alpha)\)
問７
定常波を描いてみると、中央が「腹」なのであれば、その左右\(\displaystyle\frac{\lambda}{4}\)のところに「節」がくることになります。
この位置が「原点に最も近い振幅が０になる位置」ですので、
\(\displaystyle\frac{\lambda}{4}=\frac{VT}{4}\)
\(=\displaystyle\frac{V}{4f_1}\)
となりますね。
