エネルギー保存則
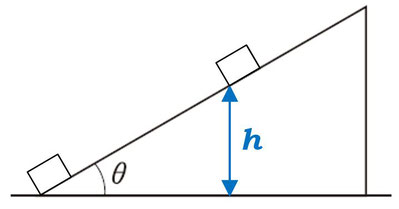
なめらかな斜面上の、高さ\(h\)のところに、質量\(m\)の物体をおいて、静かに放したとします。すると、物体は斜面上を滑って、ある速さで地面に到達します。このときの物体の地面での速さをエネルギー保存則を使って考えてみましょう。
斜面の上部と地面のそれぞれで、エネルギー状況を表にまとめてみましょう。
▼エネルギー公式
位置エネルギー
\(U=mgh\)
運動エネルギー
\(K=\frac{1}{2}mv^2\)
| 地面 | 斜面の上 | |
| 位置エネルギー |
0 |
\(mgh\) |
| 運動エネルギー | \(\frac{1}{2}mv^2\) | 0 |
| 力学的エネルギー | E | E |
重力加速度の大きさは\(g\)ということにしておきます。
力学的エネルギーは、位置エネルギーと運動エネルギーの和なので、それぞれの点における力学的エネルギーは、表から、
斜面の上:\(E=mgh+0\)
地面の上:\(E=0+\displaystyle\frac{1}{2}mv^2\)
となります。いま、摩擦や空気抵抗を無視することができるとすると、力学的エネルギーが保存しますので、\(2\)つの力学的エネルギーの大きさは等しくなります。
よって、斜面の上と地面との間での力学的エネルギー保存則より
\(mgh=\displaystyle\frac{1}{2}mv^2\)
\(×\displaystyle\frac{2}{m}\)
\(2gh=v^2\)
\(v=\sqrt{2gh}\)
となりました。
このように、力学的エネルギーの保存を利用するときは、各点での運動エネルギーや位置エネルギーを全部書き出してしまって、それを足したものがいつでも一定である、ということを利用して数式を追いかけていくのが王道です。
弾性エネルギーが関わるエネルギー保存則
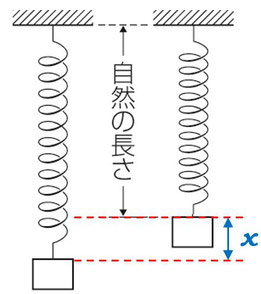
ばね定数\(k\)のばねに、質量\(m\)の物体をつるして、自然長から静かに放したとします。するとばねを伸ばしながら物体が落下していきました。ばねの長さが\(x\)だけ伸びたときの物体の速さをエネルギー保存則を使って考えてみましょう。
先ほどと同じように、図の左側と、右側とのそれぞれで、エネルギー状況を表にまとめてみましょう。左の図が、ばねが伸びて物体も動いているとき、右の図が初期状態ということにしておきます。
重力加速度の大きさは\(g\)ということにしておいて、高さの基準面は、初期位置の高さに決めておきます。
▼エネルギー公式
位置エネルギー
\(U=mgh\)
運動エネルギー
\(K=\frac{1}{2}mv^2\)
弾性エネルギー
\(U=\frac{1}{2}kx^2\)
| 左の図 | 右の図 | |
| 位置エネルギー |
\(-mgx\) |
0 |
| 運動エネルギー | \(\frac{1}{2}mv^2\) | 0 |
| 弾性エネルギー | \(\frac{1}{2}kx^2\) | 0 |
| 力学的エネルギー | E | E |
力学的エネルギーは、位置エネルギーと運動エネルギーの和なので、それぞれの点における力学的エネルギーは、表から、
右の図:\(E=0+0+0\)
左の図:\(E=-mgx+\displaystyle\frac{1}{2}mv^2+\frac{1}{2}kx^2\)
となります。いま、摩擦や空気抵抗を無視することができるとすると、力学的エネルギーが保存しますので、\(2\)つの力学的エネルギーの大きさは等しくなります。基準面の取り方の都合上、力学的エネルギーが\(0\)になっていますが、高さの基準をどこにするかは自由に決められますので、それにともなって、力学的エネルギーも正だったり、負だったり、場合によっては今のようにわざと\(0\)に設定することもできます。あれ?なんでゼロなんだ?という悩みはあまり意味がありません。そうなるように自分で決めた、ということです。
さて、図の左右での力学的エネルギー保存則より
\(-mgx+\displaystyle\frac{1}{2}mv^2+\frac{1}{2}kx^2=0\)
\(×\displaystyle\frac{2}{m}\)
\(-2gx+v^2+\displaystyle\frac{k}{m}x^2=0\)
\(v^2=2gx-\displaystyle\frac{k}{m}x^2\)
\(v=\sqrt{2gx-\displaystyle\frac{k}{m}x^2}\)
となりました。
設定が複雑になったとしても、結局やるべきことは、考えたい\(2\)点での力学的エネルギーをそれぞれ表に書き出してしまって、それらの和が等しくなることを立式してやればいいわけです。
ここでの講座ではすべて文字で説明しましたので、ちょっと分からんかったわーという人もいるでしょう。ですが、押さえておいてほしいのは、表を作って、それぞれのエネルギーの値を埋めていく、という作業をすることで解きやすさや凡ミスが格段に減る、ということです。
問題演習を通して理解を深めていきましょう。
