電気力線
電場の様子を表すために、電気力線という概念を導入しましたが、もう少し数学的に厳密にルールを決めておこうと思います。

ある面があったとして、その面\(1m^2\)をつらぬく電気力線が\(1\)本だけ存在しているとしたとき、この面上での電場の強さを\(1N/C\)と決めることにします。すると、\(1m^2\)を\(n\)本の電気力線が貫いていれば、電場は\(n[N/C]\)ということになりますね。\(S[m^2]\)を\(n\)本が貫いていれば、電場の強さは \(\displaystyle\frac{n}{S}[N/C]\)です。ということは、電場の強さを\(E\)、電気力線が貫く面積を\(S\)、総本数を\(N\)とすれば、電気力線の総本数は\(N=ES\)で表せるということです。\(1m^2\)あたり\(E\)本だから、\(S[m^2]\)あたりで考えると\(ES[本]\)ということですね。これを活用して、点電荷から飛び出てくる電気力線の総本数が何本なのかを考えていこうと思います。
Gaussの法則
ある電気量\(Q\)をもった点電荷の周囲を半径\(r\)の球殻で囲むことを考えます。点電荷から半径\(r\)だけ離れた点での電場の強さは、\(E=k_0\displaystyle\frac{Q}{r^2}\)です。これは、電気力線と面積のルールから、半径\(r\)だけ離れたところに\(1m^2\)の面があったとすると、その面を\(k_0\displaystyle\frac{Q}{r^2}\)本の電気力線が貫いている、という意味になります。
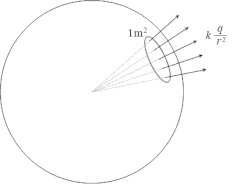
いま、点電荷をぐるっと一周まるまる球殻で囲みましたから、囲んだ部分の面積はちょうど球の表面積に相当するわけです。半径\(r\)の球の表面積\(S\)は\(S=4\pi r^2\)です。あとは、電気力線の総本数を求めるだけ。
\(N=ES\)より、\(N= k_0\displaystyle\frac{Q}{r^2} ×4\pi r^2\)ですから、結局\(r^2\)は約分されて消えてしまって、\(N=4\pi k_0Q[本]\)となります。
計算した結果、\(r\)がなくなったことはとても好都合です。はじめ、球殻の中心に点電荷が存在していて、点電荷から球殻の表面まではどこでも半径\(r\)である前提で話を進めましたが、結果的にその前提としていた\(r\)は式の中に現れてこない、つまり不要なわけです。だから、球殻内であれば、中心だろうと端っこの方だろうと関係なく、ある点電荷\(Q\)の周囲にはいつでも\(4\pi k_0Q本\)の電気力線が出る、ということが分かったのです。

\(k_0=\displaystyle\frac{1}{4\pi \varepsilon_0}\)であることを思い出すと、総本数\(N\)は\(N=\displaystyle\frac{Q}{\varepsilon_0}[本]\)と、少しシンプルな表現で書くこともできます。学問的には、こっちの簡単な表現で書く式の方が価値が高いんですけど、入試では\(k_0\)を使った問題の方が割合多い気がします。逆に\(\varepsilon\)バージョンの問題が出ると急に正答率が下がっているような気もします。覚えて済む話なら、両方覚えとくのがベストでしょう。
▼点電荷が出す電気力線数
\(N=4\pi k_0Q [本]\)
